My watch list

Monin-Obukhov Length

The Monin-Obukhov Length is the height above ground, where mechanically produced (by vertical shear) turbulence is in balance with the dissipative effect of negative buoyancy, thus where Richardson number equals to 1:

Additional recommended knowledge

Safe Weighing Range Ensures Accurate Results

How to quickly check pipettes?

How to ensure accurate weighing results every day?

$L = - \frac{u^3_*\bar\theta_v}{kg(\overline {w^'\theta^'_v})}$

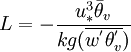
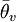where $u *$ is the frictional velocity, $\bar\theta_v$ is the mean potential virtual temperature, 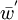$\bar w^'$ is the perturbation scalar velocity' and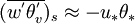 $θ *$ is a potential temperature scale (k). This can be further reduced using the similarity theory approximation:

$(\overline{w^'\theta^'_v})_s\approx-u_*\theta_*$

to give:

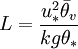
$L = \frac{u^2_*\bar\theta_v}{kg\theta_*}$

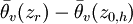The parameter $θ *$ is proportional to $\bar \theta_v (z_r) - \bar \theta_v (z_{0,h})$ the vertical difference in potential virtual temperature. The greater 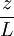$\bar \theta_v$ at $Z 0, h$ in comparison with its value at $Z r$ , the more negative the change in $\bar \theta_v$ with increasing height, and the greater the instability in the of the surface layer. In such cases, L is negative with a small magnitude, since it is inversely proportional to $u *$ . When L is negative with a small magnitude, $\frac{z}{L}$ is negative with a large magnitude. Such values of $\frac{z}{L}$ correspond to large instability due to buoyancy. Positive values of $\frac{z}{L}$ correspond to increasing $\bar \theta_v$ with altitude and stable stratification.