To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Mueller calculusMueller calculus is a matrix method for manipulating Stokes vectors, which represent the polarization of incoherent light. It was developed in 1943 by Hans Mueller, then a professor of physics at the Massachusetts Institute of Technology. Light which is unpolarized or partially polarized must be treated using Mueller calculus, while fully polarized light can be treated with either Mueller calculus or the simpler Jones calculus. Coherent light generally must be treated with Jones calculus because the latter works with amplitude rather than intensity of light. The effect of a particular optical element is represented by a Mueller matrix; which is a 4×4 matrix and a generalization of the Jones matrix. Product highlightAny fully polarized, partially polarized, or unpolarized state of light can be represented by a Stokes vector ( If a beam of light is initially in the state If a beam of light passes through optical element M1 followed by M2 then M3 it is written given that matrix multiplication is associative it can be written Beware, matrix multiplication is not commutative, so in general Below are listed the Mueller matrices for some ideal common optical elements:
See also |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Mueller_calculus". A list of authors is available in Wikipedia. |





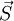 ). Any optical element can be represented by a Mueller matrix (M).
). Any optical element can be represented by a Mueller matrix (M).
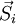 and then passes through an optical element M and comes out in a state
and then passes through an optical element M and comes out in a state 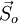 , then it is written
, then it is written
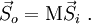
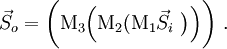
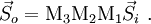
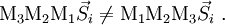
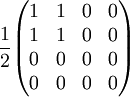 Linear polarizer (Horizontal Transmission)
Linear polarizer (Horizontal Transmission)
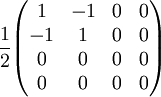 Linear polarizer (Vertical Transmission)
Linear polarizer (Vertical Transmission)
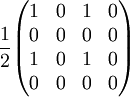 Linear polarizer (+45° Transmission)
Linear polarizer (+45° Transmission)
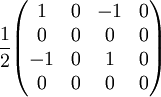 Linear polarizer (-45° Transmission)
Linear polarizer (-45° Transmission)
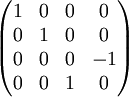 Quarter
Quarter 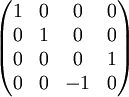 Quarter
Quarter 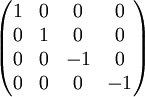 Half
Half 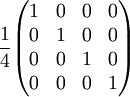 Attenuating filter (25% Transmission)
Attenuating filter (25% Transmission)


