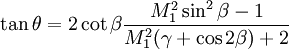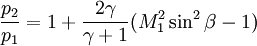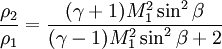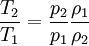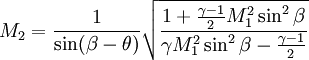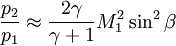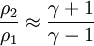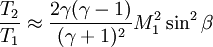My watch list
my.chemeurope.com  

my.chemeurope.com

With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.

  • My watch list
  • My saved searches
  • My saved topics
  • My newsletter
Register free of charge
Login  
eng  
DeutschEnglishFrançaisEspañol

Oblique shock



 An oblique shock wave, unlike a normal shock, is inclined with respect to the incident upstream flow direction. It will occur when a supersonic flow encounters a corner that effectively turns the flow into itself and compresses. The upstream streamlines are uniformly deflected after the shock wave. The most common way to produce an oblique shock wave is to place a wedge into supersonic, compressible flow. Similar to a normal shock wave, the oblique shock wave consists of a very thin region across which nearly discontinuous changes in the thermodynamic properties of a gas occur. While the upstream and downstream flow directions are unchanged across a normal shock, they are different for flow across an oblique shock wave.

It is always possible to convert an oblique shock into a normal shock by a Galilean transformation.

Contents

Oblique Shock Wave Theory

   For a given Mach number, M1, and corner angle, θ, the oblique shock angle, β, and the downstream Mach number, M2, can be calculated. M2 is always less than M1. Unlike after a normal shock, M2 can still be supersonic. Discontinuous changes also occur in the pressure, density and temperature, which all rise downstream of the oblique shock wave.

Using the continuity equation and the fact that the tangential velocity component does not change across the shock, trigonometric relations eventually lead to the θ-β-M equation which shows θ as a function of M1 and β. It is more intuitive to want to solve for β as a function of M1 and θ, but this approach is more complicated, the results of which are often contained in tables or calculated through an applet.


\tan \theta = 2\cot\beta\frac{M_1^2\sin^2\beta-1}{M_1^2(\gamma+\cos2\beta)+2}


Within the θ-β-M equation, a maximum corner angle, θMAX, exists for any upstream Mach number. When θ > θMAX, the oblique shock wave is no longer attached to the corner and is replaced by a detached bow shock. A θ-β-M diagram, common in most compressible flow textbooks, shows a series of curves that will indicate θMAX for each Mach number. The θ-β-M relationship will produce two β angles for a given θ and M1, with the larger angle called a strong shock and the smaller called a weak shock. The weak shock is almost always seen experimentally.

The rise in pressure, density, and temperature after an oblique shock can be calculated as follows:


\frac{p_2}{p_1} = 1+\frac{2\gamma}{\gamma+1}(M_1^2\sin^2\beta-1)


\frac{\rho_2}{\rho_1} = \frac{(\gamma+1)M_1^2\sin^2\beta}{(\gamma-1)M_1^2\sin^2\beta+2}


\frac{T_2}{T_1} = \frac{p_2}{p_1}\frac{\rho_1}{\rho_2}

M2 is solved for as follows:


M_2 = \frac{1}{\sin(\beta-\theta)}\sqrt{\frac{1+\frac{\gamma-1}{2}M_1^2 \sin^2 \beta}{\gamma M_1^2 \sin^2 \beta- \frac{\gamma-1}{2}}}

Oblique Shock Wave Applications

Oblique shock waves are used predominantly in engineering applications when compared with normal shock waves. This can be attributed to the fact that using one or a combination of oblique shock waves results in more favorable post-shock conditions (lower post-shock temperature, etc.) when compared to utilizing a single normal shock. An example of this technique can be seen in the design of supersonic aircraft engine inlets, which are wedge-shaped to compress air flow into the combustion chamber while minimizing thermodynamic losses. Early supersonic aircraft jet engine inlets were designed using compression from a single normal shock, but this approach caps the maximum achievable Mach number to roughly 1.6. The wedge-shaped inlets are clearly visible on the sides of the F-14 Tomcat, which has a maximum speed of Mach 2.34.

Many supersonic aircraft wings are designed around a thin diamond shape. Placing a diamond-shaped object at an angle of attack relative to the supersonic flow streamlines will result in two oblique shocks propagating from the front tip over the top and bottom of the wing, with Prandtl-Meyer expansion fans created at the two corners of the diamond closest to the front tip. When correctly designed, this generates lift.

Oblique Shock Waves and the Hypersonic Limit

As the Mach number of the upstream flow becomes hypersonic, the equations for the pressure, density, and temperature after the oblique shock wave reach a limit (mathematics). The pressure and density ratios can then be expressed as:


\frac{p_2}{p_1} \approx \frac{2\gamma}{\gamma+1}M_1^2\sin^2\beta


\frac{\rho_2}{\rho_1} \approx \frac{\gamma+1}{\gamma-1}


For a perfect atmospheric gas approximation using γ = 1.4, the hypersonic limit for the density ratio is 6. However, hypersonic post-shock dissociation of O2 and N2 into O and N lowers γ, allowing for higher density ratios in nature. The hypersonic temperature ratio is:


\frac{T_2}{T_1} \approx \frac{2\gamma(\gamma-1)}{(\gamma+1)^2}M_1^2\sin^2\beta


See also

References

  • Liepmann, Hans W.; Roshko, A. [1957] (2001). Elements of Gasdynamics. Dover Publications. ISBN 0-486-41963-0. 
  • Anderson, John D. Jr. [1984] (January 2001). Fundamentals of Aerodynamics, 3rd Edition, McGraw-Hill Science/Engineering/Math. ISBN 0-07-237335-0. 
  • Shapiro, Ascher H. [1953]. The Dynamics and Thermodynamics of Compressible Fluid Flow, Volume 1. Ronald Press. ISBN 978-0-471-06691-0. 
 
This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Oblique_shock". A list of authors is available in Wikipedia.
Your browser is not current. Microsoft Internet Explorer 6.0 does not support some functions on Chemie.DE