To use all functions of this page, please activate cookies in your browser.
My watch list
my.chemeurope.com
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Moving shockA Moving Shock is a Shock wave that is traveling through a fluid (usually gaseous) medium with a velocity relative to the velocity of the fluid already making up the medium. As such, the Normal shock relations require modification to calculate the properties before and after the moving shock. A knowledge of moving shocks is important for studying the phenomena surrounding detonation, among other applications. Additional recommended knowledgeTheoryTo derive the theoretical equations for a moving shock, one may start by denoting the region in front of the shock as subscript 1, with the subscript 2 defining the region behind the shock. This is shown in the figure, with the shock wave propagating to the right. The speed of the shock wave relative to the gas is W, making the total velocity equal to u1 + W. Additionally, the pressure is denoted by p and the local speed of sound by a. Next, suppose a reference frame is then fixed to the shock so it appears stationary as the gas in regions 1 and 2 move with a velocity relative to it. Redefining region 1 as x and region 2 as y leads to the following shock-relative velocities:
With these shock-relative velocities, the properties of the regions before and after the shock can be defined below introducing the Temperature as T, the density as ρ, and the Mach number as M:
Introducing the Heat capacity ratio as γ, the speed of sound, density, and pressure ratios can be derived:
One must keep in mind that the above equations are for a shock wave moving towards the right. For a shock moving towards the left, the x and y subscripts must be switched and:
See also
ReferencesShapiro, Ascher H., Dynamics and Thermodynamics of Compressible Fluid Flow, Krieger Pub. Co; Reprint ed., with corrections (June 1983), ISBN-10: 0898745667. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Moving_shock". A list of authors is available in Wikipedia. |
; 
; 
; 
; 
; 
; 
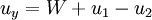
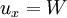
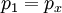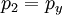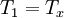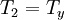
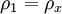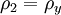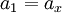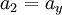
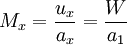
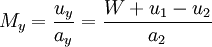
![\ \frac{a_2}{a_1} = \sqrt{1 + \frac{2(\gamma - 1)}{(\gamma + 1)^2}\left[\gamma M_x^2 - \frac{1}{M_x^2} - (\gamma - 1)\right]}](images/math/a/4/d/a4db30feac199bda5db488ed2a2056c3.png)
![\ \frac{\rho_2}{\rho_1} = \frac{1}{1-\frac{2}{\gamma + 1}\left[1 - \frac{1}{M_x^2}\right]}](images/math/c/1/e/c1ec34345fc8dcc357048749b8f4c948.png)
![\ \frac{p_2}{p_1} = 1 + \frac{2\gamma}{\gamma + 1}\left[M_x^2 - 1\right]](images/math/f/5/7/f5775bb29742669cf458551c3753c877.png)
