To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Papkovich-Neuber solutionThe Papkovich-Neuber solution is a technique for solving the Newtonian incompressible Stokes equations analytically. It can be shown that any Stokes flow with body force where |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Papkovich-Neuber_solution". A list of authors is available in Wikipedia. |


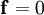 can be written in the form:
can be written in the form:
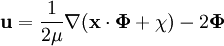
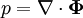
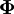 is a harmonic vector potential and
is a harmonic vector potential and 

