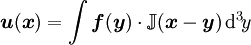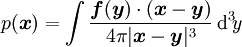To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Stokes flowStokes flow (named after George Gabriel Stokes) is a type of fluid flow where inertial forces are small compared with viscous forces. The Reynolds number is low, i.e. Product highlight
Stokes equationsFor this type of flow, the inertial forces are assumed to be negligible and the Navier-Stokes equations simplify to give the Stokes equations: where PropertiesThe Stokes Equations represent a considerable simplification of the full Navier-Stokes Equations, especially in the incompressible Newtonian case.
While these properties are true for incompressible Newtonian Stokes flows, the non-linear and sometimes time-dependent nature of Non-Newtonian fluids means that they do not hold in the more general case. Methods of solutionBy streamfunctionIt can be shown that in 2-D, the streamfunction for an incompressible Newtonian Stokes flow satisfies the Biharmonic Equation In the 3-D axisymmetric case, the streamfunction Ψ solves the equation E2Ψ = 0, where By Papkovich-Neuber solutionThe Papkovich-Neuber Solution represents the velocity and pressure fields of an incompressible Newtonian Stokes flow in terms of two harmonic potentials. By Boundary element methodCertain problems, such as the evolution of the shape of a bubble in a Stokes flow, are conducive to numerical solution by the Boundary Element method. This technique can be applied in both 2- and 3-dimensional flows. By Green's functionThe linearity of the Stokes equations in the case of an incompressible Newtonian fluid means that a Green's function for the equations can be found. The solution for the pressure p and velocity where is a second-rank tensor known as the Oseen Tensor (after Carl Wilhelm Oseen). The solution for a distributed force density See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Stokes_flow". A list of authors is available in Wikipedia. |


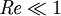 . This is a typical situation in flows where the fluid velocities are very slow, the viscosities are very large, or the length-scales of the flow are very small, such as in
. This is a typical situation in flows where the fluid velocities are very slow, the viscosities are very large, or the length-scales of the flow are very small, such as in 


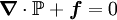
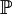 is the comoving stress tensor, and
is the comoving stress tensor, and 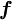 an applied body force. There is also an equation for conservation of mass. In the common case of an incompressible
an applied body force. There is also an equation for conservation of mass. In the common case of an incompressible 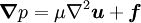
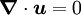
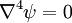 .
.
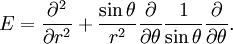
 due to a point force
due to a point force 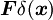 acting at the origin with
acting at the origin with 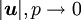 as
as 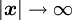 is given by
is given by
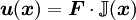
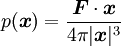
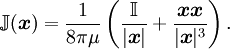
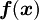 (again with decay at infinity) can then be constructed by superposition:
(again with decay at infinity) can then be constructed by superposition: