To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Parastatistics
In quantum mechanics and statistical mechanics, parastatistics is one of several alternatives to the better known particle statistics models (Bose-Einstein statistics, Fermi-Dirac statistics and Maxwell-Boltzmann statistics). Other alternatives include anyonic statistics and braid statistics, both of these involving lower spacetime dimensions. Product highlight
FormalismConsider the operator algebra of a system of N identical particles. This is a *-algebra. There is an SN group (symmetric group of order N) acting upon the operator algebra with the intended interpretation of permuting the N particles. Quantum mechanics requires focus on observables having a physical meaning, and the observables would have to be invariant under all possible permutations of the N particles. For example in the case N=2, R2-R1 cannot be an observable because it changes sign if we switch the two particles, but the distance between the two particules : |R2-R1| is a legitimate observable. In other words, the observable algebra would have to be a *-subalgebra invariant under the action of SN (noting that this does not mean that every element of the operator algebra invariant under SN is an observable). Therefore we can have different superselection sectors, each parameterized by a Young diagram of SN. In particular:
The quantum field theory of parastatisticsA paraboson field of order p, A parafermion field Explaining ParastatisticsNote that if x and y are spacelike-separated points, φ(x) and φ(y) neither commute nor anticommute unless p=1. The same comment applies to ψ(x) and ψ(y). So, if we have n spacelike separated points x1, ..., xn, corresponds to creating n identical parabosons at x1,..., xn. Similarly, corresponds to creating n identical parafermions. Because these fields neither commute nor anticommute and gives distinct states for each permutation π in Sn. We can define a permutation operator and respectively. This can be shown to be well-defined as long as QCD can be reformulated using parastatistics with the quarks being parafermions of order 3 and the gluons being parabosons of order 8. Note this is different from the conventional approach where quarks always obey anticommutation relations and gluons commutation relations. See also
|
|||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Parastatistics". A list of authors is available in Wikipedia. |





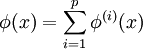 where if x and y are spacelike-separated points,
where if x and y are spacelike-separated points, 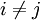 where [,] is the commutator and {,} is the anticommutator. Note that this disagrees with the spin-statistics theorem, which is for
where [,] is the commutator and {,} is the anticommutator. Note that this disagrees with the spin-statistics theorem, which is for 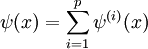 of order p, where if x and y are spacelike-separated points,
of order p, where if x and y are spacelike-separated points, 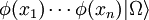
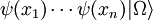
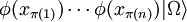
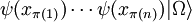
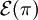 by
by
![\mathcal{E}(\pi)\left[\phi(x_1)\cdots \phi(x_n)|\Omega\rangle\right]=\phi(x_{\pi^{-1}(1)})\cdots \phi(x_{\pi^{-1}(n)})|\Omega\rangle](images/math/1/9/b/19b0b6434914d2f7946ee7c365c6dca6.png)
![\mathcal{E}(\pi)\left[\psi(x_1)\cdots \psi(x_n)|\Omega\rangle\right]=\psi(x_{\pi^{-1}(1)})\cdots \psi(x_{\pi^{-1}(n)})|\Omega\rangle](images/math/b/6/d/b6da9b5419bca9e747acab2afcd0187f.png)
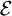 is an operator-valued representation of the symmetric group Sn and as such, we can interpret it as the action of Sn upon the n-particle Hilbert space itself, turning it into a unitary representation.
is an operator-valued representation of the symmetric group Sn and as such, we can interpret it as the action of Sn upon the n-particle Hilbert space itself, turning it into a unitary representation.


