To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Plateau's problemIn mathematics, Plateau's problem is to show the existence of a minimal surface with a given boundary, a problem raised by Joseph-Louis Lagrange in 1760. However, it is named after Joseph Plateau who was interested in soap films. The problem is considered part of the calculus of variations. The existence and regularity problems are part of geometric measure theory. Product highlightVarious specialized forms of the problem were solved, but it was only in 1930 that general solutions were found independently by Jesse Douglas and Tibor Rado. Their methods were quite different; Rado's work built on the previous work of Garnier and held only for rectifiable simple closed curves, whereas Douglas used completely new ideas with his result holding for an arbitrary simple closed curve. Both relied on setting up minimization problems; Douglas minimized the now-named Douglas integral while Rado minimized the "energy". Douglas went on to be awarded the Fields medal in 1936 for his efforts. The extension of the problem to higher dimensions (that is, for k-dimensional surfaces in n-dimensional space) turns out to be much more difficult to study. Moreover, while the solutions to the original problem are always regular, it turns out that the solutions to the extended problem may have singularities if To solve the extended problem, the theory of perimeters (De Giorgi) for boundaries and the theory of rectifiable currents (Federer and Fleming) have been developed. See also
References
This article incorporates material from Plateau's Problem on PlanetMath, which is licensed under the GFDL. |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Plateau's_problem". A list of authors is available in Wikipedia. |





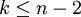 . In the hypersurface case where
. In the hypersurface case where
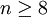 .
.


