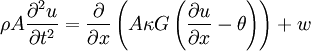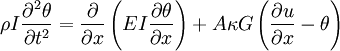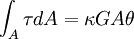Timoshenko beam theory

Additional recommended knowledge

Weighing the right way

Guide to balance cleaning: 8 simple steps

Daily Visual Balance Check

The Timoshenko beam theory was developed by Ukrainian/Russian-born scientist Stephen Timoshenko in the beginning of the 20th century. The model takes into account shear deformation and rotational inertia effects, making it suitable for describing the behaviour of short beams, sandwich composite beams or beams subject to high-frequency excitation when the wavelength approaches the thickness of the beam. The resulting equation is of 4^th order, but unlike ordinary beam theory - i.e. Bernoulli-Euler theory - there is also a second order spatial derivative present. Physically, taking into account the added mechanisms of deformation effectively lowers the stiffness of the beam, why the result is a larger deflection under a static load and lower predicted eigenfrequencies for a given set of boundary conditions. The latter effect is more noticeable for higher frequencies as the wavelength becomes shorter, and thus the distance between opposing shear forces decreases.

If the shear modulus of the beam material approaches infinity - and thus the beam becomes rigid in shear - and if rotational inertia effects are neglected, Timoshenko beam theory converges towards ordinary beam theory.

This beam theory, allowing for vibrations, may be described with the coupled linear partial differential equations ^[1]:

where the dependent variables are u, the translational displacement of the beam, and θ, the angular displacement. Note that unlike the Euler-Bernoulli theory, the angular deflection is another variable and not approximated by the slope of the deflection. Also,

• ρ is the density of the beam material (but not the linear density).
• A is the cross section area.
• E is the elastic modulus.
• G is the shear modulus.
• I is the second moment of area.
• κ, called the Timoshenko shear coefficient, depends on the geometry. Normally, κ = 5 / 6 for a rectangular section.
• w is a distributed load (force per length).

These parameters are not necessarily constants.

Determining the shear coefficient is not straightforward (nor are the determined values widely accepted, ie there's more than one answer), generally it must satisfy:

See also

• Beam theory

References

• Stephen P. Timoshenko (1932). Schwingungsprobleme der technik. Verlag von Julius Springer.