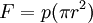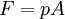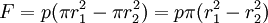My watch list

Pneumatic cylinder

The term air cylinder can also refer to a gas cylinder used to store compressed air, including those used for scuba diving.

Pneumatic cylinders (sometimes known as air cylinders) are mechanical devices which produce force, often in combination with movement, and are powered by compressed gas (typically air).

To perform their function, pneumatic cylinders impart a force by converting the potential energy of compressed gas into kinetic energy. This is achieved by the compressed gas being able to expand, without external energy input, which itself occurs due to the pressure gradient established by the compressed gas being at a greater pressure than the atmospheric pressure. This air expansion forces a piston to move in the desired direction.

Additional recommended knowledge

Daily Visual Balance Check

Weighing the right way

Correct Test Weight Handling Guide: 12 Practical Tips

1 Composition and structure
2 Operation
3 Types
4 Misc
5 See also

Composition and structure

Apart from the cylinder barrel (which is the body of the cylinder itself), a typical cylinder will include a piston and piston rod.

Operation

General

Once actuated, compressed air enters into the tube at one end of the piston and, hence, imparts force on the piston. Consequently, the piston becomes displaced (moved) by the compressed air expanding in an attempt to reach atmospheric pressure.

Specialized functions

Depending upon the design of the system, pneumatic cylinders can operate in a variety of ways. Examples include having the ability to perform multiple strokes without the need for intermediate intervention, to perform a full stroke with intermediate stopping points, to be adjusted so as to control the amount of extension and/or retraction of the piston rod once actuated.

Fail safe mechanisms

Pneumatic systems are often found in settings where even rare and brief system failure is unacceptable. In such situations locks can sometimes serve as a safety mechanism in case of loss of air supply (or its pressure falling) and, thus, remedy or abate any damage arising in such a situation.

Types

Although pneumatic cylinders will vary in appearance, size and function, they generally fall into one of the specific categories shown below. However there are also numerous other types of pneumatic cylinder available, many of which are designed to fulfill specific and specialised functions.

Single acting cylinders

Single acting cylinders (SAC) use the force imparted by air to move in one direction (usually out), and a spring to return to the "home" position

Double acting cylinders

Double Acting Cylinders (DAC) use the force of air to move in both extend and retract strokes. They have two ports to allow air in, one for outstroke and one for instroke.

Other types

Although SACs and DACs, are the most common types of pneumatic cylinder the following types are not particularly rare:

Rotary air cylinders: actuators that use air to impart a rotary motion
Rodless air cylinders: actuators that use a mechanical or magnetic coupling to impart force, typically to a table or other body that moves along the length of the cylinder body, but does not extend beyond it.

Sizes

Air cylinders are available in a variety of sizes and can typically range from a small 2.5mm air cylinder, which might be used for picking up a small transistor or other electronic component, to 400mm diameter air cylinders which would impart enough force to lift a car. Some pneumatic cylinders reach 1000mm in diameter, and are used in place of hydraulic cylinders for special circumstances where leaking hydraulic oil could impose an extreme hazard.

Pressure, radius, area and force relationships

Although the diameter of the piston and the force exerted by a cylinder are related, they are not directly proportional to one another. Additionally, the typical mathematical relationship between the two assumes that the air supply does not become saturated. Due to the effective cross sectional area reduced by the area of the piston rod, the instroke force is less than the outstroke force when both are powered pneumatically and by same supply of compressed gas.

The relationship, between force on outstroke, pressure and radius, is as follows:

$F = p ( \pi r^2 )\,$

Where:

F

represents the force exerted

r

represents the radius

π

represents the transcendental and irrational constant, which is approximately equal to 3.14159.

This is derived from the relationship, between force, pressure and effective cross-sectional area, which is:

$F = p A\,$

With the same symbolic notation of variables as above, but also $A$ represents the effective cross sectional area.

On instroke, the same relationship between force exerted, pressure and effective cross sectional area applies as discussed above for outstroke. However, since the cross sectional area is less than the piston area the relationship between force, pressure and radius is different. The calculation isn't more complicated though, since the effective cross sectional area is merely that of the piston less that of the piston rod.

For instroke, therefore, the relationship between force exerted, pressure, radius of the piston, and radius of the piston rod, is as follows:

$F = p (\pi r_1^2 - \pi r_2^2) = p \pi (r_1^2 - r_2^2)$

Where:

F

represents the force exerted

r 1

represents the radius of the piston

r 2

represents the radius of the piston rod

π

represents the transcendental and irrational constant approximately equal to 3.14159.

Misc

Pneumatic cylinders are generally less expensive than hydraulic or electric cylinders of similar size and capacity.