To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Rankine-Hugoniot equation
The Rankine-Hugoniot equation governs the behaviour of shock waves normal to the oncoming flow. It is named after physicists William John Macquorn Rankine and Pierre Henri Hugoniot, French engineer, 1851-1887. Product highlightThe idea is to consider one-dimensional, steady flow of a fluid subject to the Euler equations and require that mass, momentum, and energy are conserved. This gives three equations from which the two speeds, u1 and u2, are eliminated. It is usual to denote upstream conditions with subscript 1 and downstream conditions with subscript 2. Here, ρ is density, u speed, p pressure. The symbol e means internal energy per unit mass; thus if ideal gases are considered, the equation of state is p = ρ(γ − 1)e. The following equations are equivalent to the conservation of mass, momentum, and energy respectively. Note the three components to the energy flux: mechanical work, internal energy, and kinetic energy. Sometimes, these three conditions are referred to as the Rankine-Hugoniot conditions. Eliminating the speeds gives the following relationship: where Thus, because the pressures are both positive, the density ratio is never greater than (γ + 1) / (γ − 1), or about 6 for air (in which γ is about 1.4). As the strength of the shock increases, the downstream gas becomes hotter and hotter, but the density ratio ρ2 / ρ1 approaches a finite limit of 4 for a monatomic gas (γ = 5/3) and 6 for a diatomic gas (γ = 1.4). |
||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Rankine-Hugoniot_equation". A list of authors is available in Wikipedia. |






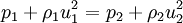
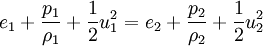
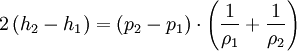
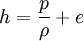 .
Now if the ideal gas equation of state is used we get
.
Now if the ideal gas equation of state is used we get