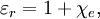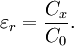To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Relative static permittivity
The relative static permittivity (or static relative permittivity) of a material under given conditions is a measure of the extent to which it concentrates electrostatic lines of flux. It is the ratio of the amount of stored electrical energy when a potential is applied, relative to the permittivity of a vacuum. The relative static permittivity is the same as the relative permittivity evaluated for a frequency of zero. The relative static permittivity is represented as εr or sometimes κ or K or Dk. It is defined as where εs is the static permittivity of the material, and ε0 is vacuum permittivity. (The relative permittivity is the complex frequency-dependent Another term for the relative static permittivity is the dielectric constant, or the relative dielectric constant, or the static dielectric constant. These terms, while they remain very common, are ambiguous and have been deprecated by some standards organizations.[6][7] The reason for the potential ambiguity is twofold. First, some older authors used "dielectric constant" or "absolute dielectric constant" for the absolute permittivity By definition, the relative permittivity of vacuum, where The static relative permittivity of a medium is related to its static electric susceptibility, χe by in SI units. Product highlight
MeasurementThe relative static permittivity εr can be measured for static electric fields as follows: first the capacitance of a test capacitor C0 is measured with vacuum between its plates. Then, using the same capacitor and distance between its plates the capacitance Cx with a dielectric between the plates is measured. The relative dielectric constant can be then calculated as For time-variant electromagnetic fields, this quantity becomes frequency dependent and in general is called relative permittivity. Practical relevanceThe dielectric constant is an essential piece of information when designing capacitors, and in other circumstances where a material might be expected to introduce capacitance into a circuit. If a material with a high dielectric constant is placed in an electric field, the magnitude of that field will be measurably reduced within the volume of the dielectric. This fact is commonly used to increase the capacitance of a particular capacitor design. The layers beneath etched conductors in Printed Circuit Boards (PCBs) also act as dielectrics. Dielectrics are used in RF transmission lines. In a coaxial cable, polyethylene can be used between the center conductor and outside shield. It can also be placed inside waveguides to form filters. Optical fibers are examples of dielectric waveguides. They consist of dielectric materials that are purposely doped with impurities so as to control the precise value of εr within the cross-section. This controls the refractive index of the material and therefore also the optical modes of transmission. However, in these cases it is technically the relative permittivity that matters, as they are not operated in the electrostatic limit. Chemical applicationsThe dielectric constant of a solvent is a relative measure of its polarity. For example, water (very polar) has a dielectric constant of 80.10 at 20 °C while n-hexane (very non-polar) has a dielectric constant of 1.89 at 20 °C.[10] This information is of great value when designing separation, sample preparation and chromatography techniques in analytical chemistry. See also
References
Categories: Electric and magnetic fields in matter | Colloidal chemistry |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Relative_static_permittivity". A list of authors is available in Wikipedia. |


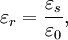
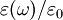 , which gives the static relative permittivity for
, which gives the static relative permittivity for 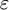 rather than the relative permittivity.
rather than the relative permittivity.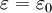 , is equal to 1.
, is equal to 1.