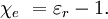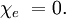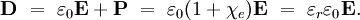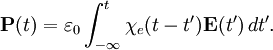To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Electric susceptibilityThe electric susceptibility χe of a dielectric material is a measure of how easily it polarizes in response to an electric field. This, in turn, determines the electric permittivity of the material and thus influences many other phenomena in that medium, from the capacitance of capacitors to the speed of light. Product highlightIt is defined as the constant of proportionality (which may be a tensor) relating an electric field E to the induced dielectric polarization density P such that where The susceptibility of a medium is related to its relative permittivity So in the case of a vacuum, The electric displacement D is related to the polarization density P by Dispersion and causalityIn general, a material cannot polarize instantaneously in response to an applied field, and so the more general formulation as a function of time is That is, the polarization is a convolution of the electric field at previous times with time-dependent susceptibility given by χe(Δt). The upper limit of this integral can be extended to infinity as well if one defines χe(Δt) = 0 for Δt < 0. An instantaneous response corresponds to Dirac delta function susceptibility χe(Δt) = χeδ(Δt). It is more convenient in a linear system to take the Fourier transform and write this relationship as a function of frequency. Due to the convolution theorem, the integral becomes a simple product, This frequency dependence of the susceptibility leads to frequency dependence of the permittivity. The shape of the susceptibilty with respect to frequency characterizes the dispersion properties of the material. Moreover, the fact that the polarization can only depend on the electric field at previous times (i.e. χe(Δt) = 0 for Δt < 0), a consequence of causality, imposes Kramers-Kronig constraints on the susceptibility χe(0). See also
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Electric_susceptibility". A list of authors is available in Wikipedia. |





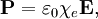
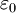 is the electric
is the electric 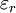 by
by