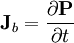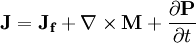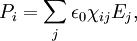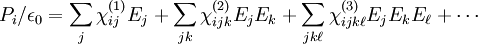To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Polarization densityIn classical electromagnetism, the polarization density (or electric polarization, or simply polarization) is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. The polarization vector P is defined as the dipole moment per unit volume. The SI unit of measure is coulombs per square metre. Product highlight
Polarization density in Maxwell's equationsThe behavior of electric fields (E, D),magnetic fields (B, H), charge density (ρ) and current density (J) are described by Maxwell's equations. The role of the polarization density P is described below. Relations between E, D and PThe polarization density P defines the electric displacement field D as which is convenient for various calculations. A relation between P and E exists in many materials, as described later in the article. Bound chargeElectric polarization corresponds to a rearrangement of the bound electrons in the material, which creates an additional charge density, known as the bound charge density ρb: so that the total charge density that enters Maxwell's equations is given by where ρf is the free charge density (describing charges brought from outside). At the surface of the polarized material, the bound charge appears as a surface charge density where
so that the total current density that enters Maxwell's equations is given by where Jf is the free-charge current density, and the second term is a contribution from the magnetization (when it exists). Relation between P and E in various materialsIn a homogeneous linear and isotropic dielectric medium, the polarization is aligned with and proportional to the electric field E. In an anisotropic material, the polarization and the field are not necessarily in the same direction. Then, the ith component of the polarization is related to the jth component of the electric field according to: where ε0 is the permittivity of free space, and χ is the electric susceptibility tensor of the medium. The case of an anisotropic dielectric medium is described by the field of crystal optics. As in most electromagnetism, this relation deals with macroscopic averages of the fields and dipole density, so that one has a continuum approximation of the dielectric materials that neglects atomic-scale behaviors. The polarizability of individual particles in the medium can be related to the average susceptibility and polarization density by the Clausius-Mossotti relation. In general, the susceptibility is a function of the frequency ω of the applied field. When the field is an arbitrary function of time t, the polarization is a convolution of the Fourier transform of χ(ω) with the E(t). This reflects the fact that the dipoles in the material cannot respond instantaneously to the applied field, and causality considerations lead to the Kramers-Kronig relations. If the polarization P is not linearly proportional to the electric field E, the medium is termed nonlinear and is described by the field of nonlinear optics. To a good approximation (for sufficiently weak fields, assuming no permanent dipole moments are present), P is usually given by a Taylor series in E whose coefficients are the nonlinear susceptibilities: where χ(1) is the linear susceptibility, χ(2) gives the Pockels effect, and χ(3) gives the Kerr effect. In ferroelectric materials, there is no one-to-one correspondence between P and E at all because of hysteresis. References and notesSee also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Polarization_density". A list of authors is available in Wikipedia. |





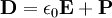
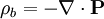
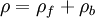
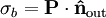
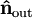 is the normal vector. If P is uniform inside the material, this surface charge is the only bound charge.
is the normal vector. If P is uniform inside the material, this surface charge is the only bound charge.