To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Electric displacement fieldIn physics, the electric displacement field or electric induction[citation needed] is a vector field Product highlightDefinitionIn general, D is defined by the relation where E is the electric field, If P can be written as a linear function of E, which is the case in most materials, it can be written as and by it yields where Displacement field in a capacitorConsider an infinite parallel plate capacitor placed in space (or in a medium) with no free charges present except on the capacitor. In SI units, the charge density on the plates is equal to the value of the D field between the plates. This follows directly from Gauss's law, by integrating over a small rectangular box straddling both plates of the capacitor: On the sides of the box, which is the charge density on the plate. Outside the capacitor, the two plates effect compensate each other and UnitsIn the standard SI system of units D is measured in coulombs per square meter (C/m²). This choice of units results in one of the simplest forms of the Ampère-Maxwell equation:
If one chooses both B and H to be measured in teslas, and E and D to be measured in newtons per coulomb, then the formula is modified to be:
Therefore it is seen as being preferential to express B & H, and E & D in different sets of units. Choice of units has differed in history, for instance in the electromagnetic system of scientific units, in which the unit of charge is defined so that |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Electric_displacement_field". A list of authors is available in Wikipedia. |


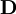 that appears in Maxwell's equations. It accounts for the effects of unbound
that appears in Maxwell's equations. It accounts for the effects of unbound 


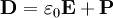
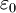 is the vacuum permittivity, and P is the
is the vacuum permittivity, and P is the 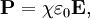
 is the
is the 
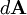 is perpendicular to the field, so that part of the integral is zero, leaving, for the space inside the capacitor where the effect of the two plates adds:
is perpendicular to the field, so that part of the integral is zero, leaving, for the space inside the capacitor where the effect of the two plates adds:
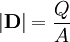
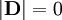 .
.
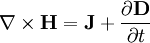
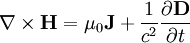
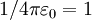 (dimensionless), E and D are expressed in the same units.
(dimensionless), E and D are expressed in the same units.


