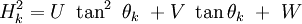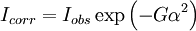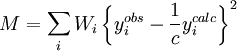To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Rietveld refinement
The Rietveld method uses a least squares approach to refine a theoretical line profile until it matches the measured profile. The introduction of this technique was a significant step forward in the diffraction analysis of powder samples as, unlike other techniques at that time, it was able to deal reliably with strongly overlapping reflections. The method was first reported for the diffraction of monochromatic neutrons where the peak position is reported in terms of the Bragg angle 2θ. This terminology will be used here although the technique is equally applicable to alternative scales such as x-ray energy or neutron time-of-flight. The only wavelength and technique independent scale is in reciprocal space units or momentum transfer Q, which is historically rarely used in powder diffraction but very common in all other diffraction and optics techniques. The relation is
Product highlight
Peak shapeThe shape of a powder diffraction peak is influenced by the characteristics of the beam, the experimental arrangement, and the sample size and shape. In the case of monochromatic neutron sources the convolution of the various effects has been found to result in a peak almost exactly Gaussian in shape. If this distribution is assumed then the contribution of a given peak to the profile yi at position 2θi is:
where Hk is the full width at half peak height (full-width half-maximum), 2θk is the centre of the peak, and Ik is the calculated intensity of the peak (determined from the structure factor, the Lorentz factor, and multiplicity of the reflection) At very low diffraction angles the peaks may acquire an asymmetry due to the vertical divergence of the beam. Reitveld used a semi-empirical correction factor, As to account for this asymmetry
where P is the asymmetry factor and s is +1,0,-1 depending on the difference 2θi-2θk being positive, zero or negative respectively. At a given position more than one diffraction peak may contribute to the profile. The intensity is simply the sum of all peaks contributing at the point 2θi. Peak widthThe width of the diffraction peaks are found to broaden at higher Bragg angles. This angular dependency was originally represented by
where U, V and W are the halfwidth parameters and may be refined during the fit. Preferred orientationIn powder samples there is a tendency for plate- or rod-like crystallites to align themselves along the axis of a cylindrical sample holder. In solid polycrystalline samples the production of the material may result in greater volume fraction of certain crystal orientations (commonly referred to as texture). In such cases the peak intensities will vary from that predicted for a completely random distribution. Rietveld allowed for moderate cases of the former by introducing a correction factor:
where Iobs is the intensity expected for a random sample, G is the preferred orientation parameter and α is the acute angle between the scattering vector and the normal of the crystallites. RefinementThe principle of the Rietveld Method is to minimise a function M which represents the difference between a calculated profile y(calc) and the observed data y(obs). Rietveld defined such an equation as:
where Wi is the statistical weight and c is an overall scale factor such that ycalc = cyobs References
Links
Categories: Crystallography | Diffraction | Neutron related techniques |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Rietveld_refinement". A list of authors is available in Wikipedia. |


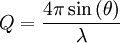



![y_i = I_k exp \left [ -4 ln \left ( \frac{2}{H_k^2} \right ) \left (2\theta_i - 2\theta_k \right )^2 \right ]](images/math/d/4/b/d4b67b0eaa86f186c0312f2d885aaa01.png)
![A_s = 1 - \left [ \frac {sP \left (2\theta_i - 2\theta_k \right )^2}{tan \theta_k} \right ]](images/math/9/9/8/998e3859e8720cf5ee0411f334026457.png)