To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Structure factorIn physics, in the area of crystallography, the structure factor of a crystal is a mathematical description of how the crystal scatters incident radiation. The structure factor is a particularly useful tool in the interpretation of interference patterns obtained in X-ray, electron and neutron diffraction experiments. Product highlightScattering from a crystalA crystal is a periodic arrangement of atoms in a particular pattern. Each of the atoms may scatter incident radiation such as X-rays, electrons and neutrons. Because of the periodic arrangement of the atoms, the interference of waves scattered from different atoms may cause a distinct pattern of constructive and destructive interference to form. This is the diffraction pattern caused by the crystal. In the kinematical approximation for diffraction, the intensity of a diffracted beam is given by: where Here, The structure factor describes the way in which an incident beam is scattered by the atoms of a crystal unit cell, taking into account the different scattering power of the elements through the term fi. Since the atoms are spatially distributed in the unit cell, there will be a difference in phase when considering the scattered amplitude from two atoms. This phase shift is taken into account by the complex exponential term. The atomic form factor, or scattering power, of an element depends on the type of radiation considered. Because electrons interact with matter though different processes than for example X-rays, the atomic form factors for the two cases are not the same. Structure factors for specific lattice typesTo compute structure factors for a specific lattice, compute the sum above over the atoms in the unit cell. Since crystals are often described in terms of their Miller indices, it is useful to examine a specific structure factor in terms of these. Body-centered cubic (BCC) As a convention, the body-centered cubic system is described in terms of a simple cubic lattice with primitive vectors In a monoatomic crystal, all the form factors f are the same. The intensity of a diffracted beam scattered with a vector We then arrive at the following result for the structure factor for scattering from a plane (hkl):
This result tells us that for a reflection to appear in a diffraction experiment involving a body-centered crystal, the sum of the Miller indices of the scattering plane must be even. If the sum of the Miller indices is odd, the intensity of the diffracted beam is reduced to zero due to destructive interference. This zero intensity for a group of diffracted beams is called a systematic absence. Since atomic form factors fall off with increasing diffraction angle corresponding to higher Miller indices, the most intense diffraction peak from a material with a BCC structure is typically the (110). The (110) plane is the most densely packed of BCC crystal structures and is therefore the lowest energy surface for a thin film to expose. Films of BCC materials like iron and tungsten therefore grow in a characteristic (110) orientation. Face-centered cubic (FCC) In the case of a monoatomic FCC crystal, the atoms in the basis are at the origin with the result
The most intense diffraction peak from a material that crystallizes in the FCC structure is typically the (111). Films of FCC materials like silicon tend to grow in a (111) orientation with a triangular surface symmetry although the surfaces of wafers on which integrated circuits are grown instead have the (100) orientation with a square surface symmetry. Diamond Crystal Structure The Diamond cubic crystal structure is possessed by diamond (carbon), most semiconductors and tin. The basis cell contains 8 atoms located at cell positions:
The Structure factor then takes on a form like this:
h+k+l is odd then F2 will be 32fSi2 h+k+l is an even multiple of 2 then F2 will be 64fSi2 h+k+l is an odd multiple of 2 then F2 will be 0 See also
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Structure_factor". A list of authors is available in Wikipedia. |





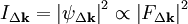
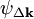 is the wavefunction of a beam scattered a vector
is the wavefunction of a beam scattered a vector 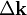 , and
, and 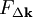 is the so called structure factor which is given by:
is the so called structure factor which is given by:
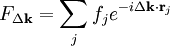
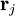 is the position of an atom
is the position of an atom 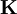 .
.
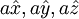 , with a basis consisting of
, with a basis consisting of 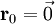 and
and 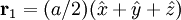 . The corresponding reciprocal lattice is also simple cubic with side
. The corresponding reciprocal lattice is also simple cubic with side 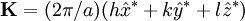 by a crystal plane with Miller indices
by a crystal plane with Miller indices ![\begin{matrix} F_{\mathbf{K}} & = & f \left[ e^{-i\mathbf{K}\cdot\vec{0}} + e^{-i\mathbf{K}\cdot(a/2)(\hat{x} + \hat{y} + \hat{z})} \right] \\ & = & f \left[ 1 + e^{-i\mathbf{K}\cdot(a/2)(\hat{x} + \hat{y} + \hat{z})} \right] \\ & = & f \left[ 1 + e^{-i\pi(h + k + l)} \right]\\ & = & f \left[ 1 + (-1)^{h + k + l} \right] \\ \end{matrix}](images/math/9/1/3/913548f520e05c1ba6cb55ae65fb2347.png)
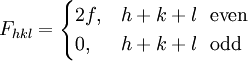
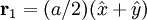 ,
, 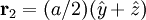 ,
, 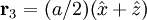 with indices given by (1/2,1/2,0), (0,1/2,1/2), (1/2,0,1/2). An argument similar to the one above gives the expression
with indices given by (1/2,1/2,0), (0,1/2,1/2), (1/2,0,1/2). An argument similar to the one above gives the expression
![\begin{matrix} F_{\mathbf{K}} & = & f \left[ e^{-i\mathbf{K}\cdot\vec{0}} + e^{-i\mathbf{K}\cdot(a/2)(\hat{x} + \hat{y})} + e^{-i\mathbf{K}\cdot(a/2)(\hat{y} + \hat{z})} + e^{-i\mathbf{K}\cdot(a/2)(\hat{x} + \hat{z})} \right] \\ & = & f \left[ 1 + (-1)^{h + k} + (-1)^{k + l} + (-1)^{h + l} \right] \\ \end{matrix}](images/math/2/f/6/2f6ab07898768498cb7e4fecabafaff9.png)
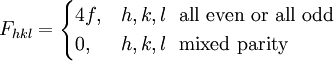
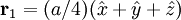
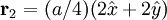
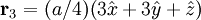
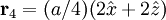
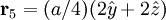
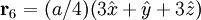
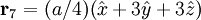
![\begin{matrix} F_{\mathbf{K}} & = & f \left[ \begin{matrix} e^{-i\mathbf{K}\cdot\vec{0}} + e^{-i\mathbf{K}\cdot(a/2)(\hat{x} + \hat{y})} + e^{-i\mathbf{K}\cdot(a/2)(\hat{y} + \hat{z})} + e^{-i\mathbf{K}\cdot(a/2)(\hat{x} + \hat{z})} + \\ e^{-i\mathbf{K}\cdot(a/4)(\hat{x} + \hat{y} + \hat{z})} + e^{-i\mathbf{K}\cdot(a/4)(3\hat{x} + \hat{y} + 3\hat{z})} + e^{-i\mathbf{K}\cdot(a/4)(3\hat{x} + 3\hat{y} + \hat{z})} + e^{-i\mathbf{K}\cdot(a/4)(\hat{x} + 3\hat{y} + 3\hat{z})} \end{matrix} \right] \\ & = & f \left[ \begin{matrix} 1 + (-1)^{h + k} + (-1)^{k + l} + (-1)^{h + l} + \\ (i)^{h + k + l} + (i)^{3h + k + 3l} + (i)^{3h + 3k + l} + (i)^{h + 3k + 3l} \end{matrix} \right] \\ & = & f \left[ 1 + (-1)^{h + k} + (-1)^{k + l} + (-1)^{h + l} \right] \cdot \left[ 1 + (i)^{h + k + l} \right]\\ \end{matrix}](images/math/8/4/e/84ea3e7b50413ea51eccf18e7d2ac051.png)


