To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Miller indexMiller indices are a notation system in crystallography for planes and directions in crystal lattices. In particular, a family of lattice planes is determined by three integers There are also several related notations.[1] Miller indices were introduced in 1839 by the British mineralogist William Hallowes Miller. The method was also historically known as the Millerian system, and the indices as Millerian,[2] although this is now rare. Product highlight
Definition
There are two equivalent ways to define the meaning of the Miller indices:[1] via a point in the reciprocal lattice, or as the inverse intercepts along the lattice vectors. Both definitions are given below. In either case, one needs to choose the three lattice vectors Then, given the three Miller indices That is, Equivalently, The related notation That is, it uses the direct lattice basis instead of the reciprocal lattice. Note that Case of the cubic structuresFor the special case of simple cubic crystals, the lattice vectors are orthogonal and of equal length; similarly for the reciprocal lattice. So, in this common case, the Miller indices For face-centered cubic and body-centered cubic lattices, the primitive lattice vectors are not orthogonal. However, in these cases the Miller indices are conventionally defined relative to the lattice vectors of the cubic Bravais lattice, and hence are again simply the Cartesian directions. Case of the hexagonal and rhombohedral structures
With hexagonal and rhombohedral crystal systems, it is possible to use the Bravais-Miller index which has 4 numbers (h k i l)
where h, k and l are identical to the Miller index. The (001) plane has a 3-fold symmetry: it remains unchanged by a rotation of 1/3 (2π/3 rad, 120°). The [100], [010] and the
i is redundant and not necessary. The crystallographic planes and directions
The crystallographic directions are fictitious lines linking nodes (atoms, ions or molecules) of a crystal. The crystallographic planes are fictitious planes linking nodes. Some directions and planes have a higher density of nodes; these dense planes have an influence on the behaviour of the crystal:
For all these reasons, it is important to determine the planes and thus to have a notation system. See alsoReferences |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Miller_index". A list of authors is available in Wikipedia. |


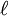 ,
, 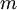 , and
, and 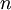 , the Miller indices. They are written
, the Miller indices. They are written 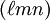 and denote planes orthogonal to a direction
and denote planes orthogonal to a direction 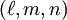 in the basis of the
in the basis of the 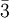 for
for ![[\ell m n]](images/math/0/a/4/0a42aaab093201b89be0823292b79a3f.png) , with square instead of round brackets, denotes a direction in the basis of the direct lattice vectors instead of the reciprocal lattice. The notation
, with square instead of round brackets, denotes a direction in the basis of the direct lattice vectors instead of the reciprocal lattice. The notation 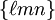 denotes all planes that are equivalent to
denotes all planes that are equivalent to 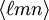 denotes all directions that are equivalent to
denotes all directions that are equivalent to 


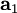 ,
, 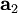 , and
, and 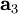 as described above. Given these, the three primitive
as described above. Given these, the three primitive 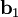 ,
, 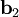 , and
, and 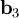 ).
).
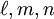 ,
, 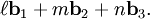
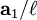 ,
, 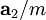 , and
, and 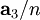 , or some multiple thereof. That is, the Miller indices are proportional to the inverses of the intercepts of the plane, in the basis of the lattice vectors. If one of the indices is zero, it means that the planes do not intersect that axis (the intercept is "at infinity").
, or some multiple thereof. That is, the Miller indices are proportional to the inverses of the intercepts of the plane, in the basis of the lattice vectors. If one of the indices is zero, it means that the planes do not intersect that axis (the intercept is "at infinity").
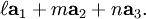
![[\bar{1}\bar{1}0]](images/math/f/6/3/f63d9d2f540541f23168efeac43cb644.png) directions are really similar. If S is the intercept of the plane with the
directions are really similar. If S is the intercept of the plane with the ![[1\bar{1}0]](images/math/8/3/2/832dfdcfb221babf477a6a8e1c48979a.png) axis, then
axis, then


