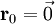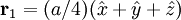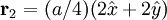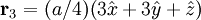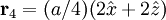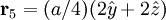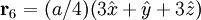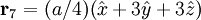To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Diamond cubic
Product highlightThe diamond cubic crystal structure is a repeating pattern that atoms may adopt as certain materials solidify. While the first known example was diamond, other elements in group IV also adopt this structure, including tin, the semiconductors silicon and germanium, and silicon/germanium alloys in any proportion. Diamond cubic is in the Fd3m space group, which follows the face-centered cubic bravais lattice. The lattice describes the repeat pattern; for diamond cubic crystals this lattice is "decorated" with a motif of two tetrahedrally bonded atoms in each primitive cell, separated by 1/4 of the width of the unit cell in each dimension. Many compound semiconductors such as gallium arsenide, β-silicon carbide and indium antimonide adopt the analogous zinc blende structure, where each atom has nearest neighbors of an unlike element. This structure's space group is F43m, but many of its structural properties are quite similar. The atomic packing factor of the diamond cubic structure is Mathematically, the points of the diamond cubic structure can be given coordinates as a subset of a three-dimensional integer lattice by using a cubical unit cell four units across. Atomic placement in unit cell of side length a is given by the following placement vectors.
See also crystallography. Manufacturing considerations
Since this class of material is important for electronics, it is important to know that they present open, hexagonal ion channels when ion implantation is carried out from any of the <110> directions (that is, 45 degrees from one of the cube edges). Their open structure also results in a volume reduction upon melting or amorphization, as is also seen in ice. They display octahedral cleavage, which means that they have four planes—directions following the faces of the octahedron where there are fewer bonds and therefore points of structural weakness—along which single crystals can easily split, leaving smooth surfaces. Similarly, this lack of bonds can guide chemical etching of the right chemistry (i.e., potassium hydroxide solutions for Si) to produce pyramidal structures such as mesas, points, or etch pits, a useful technique for MEMS.
VideoAnimations of this structure are available at Wikimedia Commons:
Categories: Condensed matter physics | Crystallography |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Diamond_cubic". A list of authors is available in Wikipedia. |





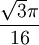 with eight atoms per unit cell.
with eight atoms per unit cell.