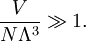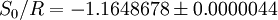To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Sackur–Tetrode equationThe Sackur–Tetrode equation is an expression for the entropy of a monatomic classical ideal gas which uses quantum considerations to arrive at an exact formula. Classical thermodynamics can only give the entropy of a classical ideal gas to within a constant. Product highlightThe Sackur–Tetrode equation is named for Hugo Martin Tetrode (1895–1931) and Otto Sackur (1880–1914), who developed it independently as a solution of Boltzmann's gas statistics and entropy equations, at about the same time in 1912. The Sackur–Tetrode equation is written: where V is the volume of the gas, N is the number of particles in the gas, U is the internal energy of the gas, k is Boltzmann's constant, m is the mass of a gas particle, h is Planck's constant and ln() is the natural logarithm. See Gibbs paradox for a derivation of the Sackur–Tetrode equation. See also the ideal gas article for the constraints placed upon the entropy of an ideal gas by thermodynamics alone. The Sackur–Tetrode equation can also be conveniently expressed in terms of the thermal wavelength Λ. Using the classical ideal gas relationship U = (3/2)NkT for a monatomic gas gives Note that the assumption was made that the gas is in the classical regime, and is described by Maxwell–Boltzmann statistics (with "correct counting"). From the definition of the thermal wavelength, this means the Sackur–Tetrode equation is only valid for and in fact, the entropy predicted by the Sackur–Tetrode equation approaches negative infinity as the temperature approaches zero. The Sackur–Tetrode constantThe Sackur–Tetrode constant, written S0 / R, is equal to S/kN evaluated at a temperature of T = 1 kelvin, at standard atmospheric pressure (101.325 kPa), for a particle of mass equal to one atomic mass unit (m = 1.6605388628x10−27 kg), which yields the dimensionless quantity: (Note: sometimes a pressure of 100 kPa is used, which yields a value of −1.15169321.) Categories: Thermodynamic entropy | Gases |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Sackur–Tetrode_equation". A list of authors is available in Wikipedia. |





![S = k N \ln \left[ \left(\frac VN\right) \left(\frac UN \right)^{\frac 32}\right]+ {\frac 32}kN\left( {\frac 53}+ \ln\frac{4\pi m}{3h^2}\right)](images/math/d/8/8/d88acc17cf6f48b9c08199b86cab7e67.png)
![\frac{S}{kN} = \ln\left[\frac{V}{N\Lambda^3}\right]+\frac{5}{2}](images/math/8/d/7/8d796f26923bbd1beeef7d52bddcf024.png)