My watch list

Secular equilibrium

In nuclear physics, secular equilibrium is a situation in which the quantity of a radioactive isotope remains constant because its production rate (due, e.g., to decay of a parent isotope) is equal to its decay rate.

Additional recommended knowledge

Daily Sensitivity Test

Weighing the right way

What is the Sensitivity of my Balance?

Secular equilibrium in radioactive decay

Secular equilibrium can only occur in a radioactive decay chain if the half-life of the daughter radionuclide B is much shorter than the half-life of the parent radionuclide A. In such a situation, the decay rate of A, and hence the production rate of B, is approximately constant, because the half-life of A is very long compared to the timescales being considered. The quantity of radionuclide B builds up until the number of B atoms decaying per unit time becomes equal to the number being produced per unit time; the quantity of radionuclide B then reaches a constant, equilibrium value.

The quantity of radionuclide B when secular equilibrium is reached is determined by the quantity of its parent A and the half-lives of the two radionuclide. This can be seen from the time rate of change of the number of atoms of radionuclide B:

$\frac{dN_B}{dt} = \lambda_A N_A - \lambda_B N_B$

where λ_A and λ_B are the decay constants of radionuclide A and B, related to their half-lives t_1/2 by $λ = l n (2) / t 1 / 2$ , and N_A and N_B are the number of atoms of A and B at a given time.

Secular equilibrium occurs when $d N B / d t = 0$ , or

$N_B = \frac{\lambda_A}{\lambda_B}N_A$

Over long enough times, comparable to the half-life of radionuclide A, the secular equilibrium is only approximate; N_A decays away according to

$N_A(t) = N_A(0) e^{-\lambda_A t}$ ,

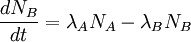
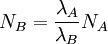
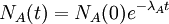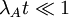and the "equilibrium" quantity of radionuclide B declines in turn. For times short compared to the half-life of A, $\lambda_A t \ll 1$ and the exponential can be approximated as 1.