To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Spectral phase interferometry for direct electric-field reconstructionIn ultrafast optics, spectral phase interferometry for direct electric-field reconstruction (SPIDER) is an ultrashort pulse measurement technique. Product highlight
The basicsSPIDER is an interferometric ultrashort pulse measurement technique in the frequency domain based on spectral shearing interferometry. Spectral shearing interferometry is similar in concept to intensity autocorrelation except that, instead of gating a pulse with a time-shifted copy of itself, a pulse is interfered with a frequency-shifted or spectrally sheared copy of itself. Because even the fastest detectors are unable to resolve ultrashort laser pulses, SPIDER uses nonlinear mixing as a combination of filters to generate a signal that can be measured by a slow detector. TheoryThere are two important specifications for filters: time/frequency response and amplitude/phase response. A filter is said to be time or frequency stationary if its output is unaffected by the time or frequency of the input. A filter can also be classified as amplitude-only or phase-only depending on its response to the amplitude or phase of the input. Because a time stationary filter and a frequency stationary filter can be combined to make a linear filter with any arbitrary response, both are a necessary and sufficient requirement for the measurement of the electric field of an input pulse. In a basic spectral shearing interferometer, the input beam is split into two identical pulses, sending one through a linear spectral phase modulator: while the other is sent through a linear temporal phase modulator: The two pulses are then recombined and sent through a spectrometer: The linear spectral phase modulator is a time stationary, phase-only filter and adds spectral shear to pulses in its arm of the interferometer. The linear temporal phase modulator is frequency stationary, phase-only filter which adds temporal delay to the pulse in its arm. The spectrometer in which the pulses are recombined is a time stationary, amplitude-only filter which resolves with pass-band γ and center frequency ωc. In this setup, the pulse through the temporal phase arm has its spectrum shifted by a spectral shear of Ω. In order to exactly measure a pulse, the field must be sampled by a certain number of spectrally sheared components. This sampling requirement is determined by the Nyquist–Shannon sampling theorem. If the function has compact support on the interval τN, then it is completely determined by giving its values at a series of frequencies 2π/τN apart. This means that the spectral shear that needs to be generated by the SPIDER is Ω = 2π/τN. The pulse through the spectral arm acquires a time-delay of τ. The recombination of the pulses from the two arms is then resolved by the spectrometer which produces a signal containing the spectrometer function, which can be approximated by a delta function due to its pass-band, γ, being so much narrower than the spectrum of the input pulse. In addition, because the spectral and temporal delays are fixed, the only remaining variable is the center frequency, ω_c, of the spectrometer. The resulting signal contains the spectrum of the input pulse, the spectrum of the sheared pulse, and the phase difference between the frequency components of the input pulse which were separated by the spectral shear. The shearing interferogram created by this signal generally consists of fringes spaced at a frequency of 2π/τ. Deviations from the nominal fringe spacing can be analyzed to obtain the spectral phase of the field. The spectral amplitude must be obtained by a separate measurement of the pulse spectrum. Experimental set-up
The two arms in a spectral shearing interferometer are implemented by means of a beam splitter (B), Diffraction grating (G), lens (L), Aperture (A), Charge-coupled device C, and a method for sum frequency generation (S). These components make up the spectrometer and optical delay line. ReferencesIaconis, C & Walmsley, I. A. (1999), " ", IEEE J. Quantum Electron. 35 (4): 501-509, DOI 10.1109/3.753654 Iaconis, C & Walmsley, I. A. (1998), " ", Opt. Lett. 23 (10): 792-794, Walmsley, I. A. & Wong, V. (1996), " ", J. Opt. Soc. Am. B 13 (11): 2453-2463, Competing techniques
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Spectral_phase_interferometry_for_direct_electric-field_reconstruction". A list of authors is available in Wikipedia. |





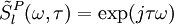
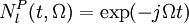
![\tilde{S}^A(\omega-\omega_c)=\exp \left [\frac{-(\omega-\omega_c)^2}{2\gamma^2} \right ]](images/math/2/8/4/28480fd978af6558ba982eab7f5776b7.png)
![S(\omega_c;\Omega,\tau) = \int \left \{ \tilde{S}^A(\omega-\omega_c) \cdot \left [ \int N_l^P(\omega'-\omega) \tilde{E}(\omega)d\omega' + \tilde{S}_l^P(\omega) \tilde{E}(\omega) \right ] \right \}^2 d\omega](images/math/2/5/9/25907e88f188c50a63651916c12bf1e7.png)
![S(\omega_c) = \left \{ \left | \tilde{E}(\omega_c - \Omega) \right |^2 + \left | \tilde{E}(\omega_c) \right |^2 + 2 \left | \tilde{E}(\omega_c-\Omega)\tilde{E}(\omega_c) \right |\cos \left [ \phi_{\omega}(\omega_c-\Omega)-\phi_{\omega}(\omega_c)-\tau\omega_c \right ] \right \}](images/math/a/6/1/a61fcc28fe687f93ee597bad2f79b430.png)


