To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Ultrashort pulseIn optics, an ultrashort pulse of light is an electromagnetic pulse whose time duration is on the order of the femtosecond (10 − 15 second). Such pulses have a broadband optical spectrum, and can be created by mode-locked oscillators. They are commonly referred to as ultrafast events. They are characterized by a high peak intensity (or more correctly, irradiance) that usually leads to nonlinear interactions in various materials, including air. These processes are studied in the field of nonlinear optics. In the specialized literature, "ultrashort" refers to the femtosecond (fs) to picosecond (ps) range, although such pulses no longer hold the record for the shortest pulses artificially generated. Indeed, pulse durations on the attosecond time scale have been reported. The 1999 Nobel Prize in Chemistry was awarded to Ahmed H. Zewail for using ultrashort pulses to observe chemical reactions on the timescales they occur on, opening up the field of femtochemistry. Product highlight
Definition
The real electric field corresponding to an ultrashort pulse is oscillating at an angular frequency ω0 corresponding to the central wavelength of the pulse. To facilitate calculations, a complex field E(t) is defined. Formally, it is defined as the analytic signal corresponding to the real field. The central angular frequency ω0 is usually explicitly written in the complex field, which may be separated as an intensity function I(t) and a phase function ψ(t): The expression of the complex electric field in the frequency domain is obtained from the Fourier transform of E(t): Because of the presence of the Just as in the time domain, an intensity and a phase function can be defined in the frequency domain: The quantity S(ω) is the spectral density (or simply, the spectrum) of the pulse, and φ(ω) is the spectral phase. Example of spectral phase functions include the case where φ(ω) is a constant, in which case the pulse is called a bandwidth-limited pulse, or where φ(ω) is a quadratic function, in which case the pulse is called a chirped pulse because of the presence of an instantaneous frequency sweep. Such a chirp may be acquired as a pulse propagates through materials (like glass) and is due to their dispersion. It results in a temporal broadening of the pulse. The intensity functions I(t) and S(ω) determine the time duration and spectral bandwidth of the pulse. As stated by the uncertainty principle, their product (sometimes called the time-bandwidth product) has a lower bound. This minimum value depends on the definition used for the duration and on the shape of the pulse. For a given spectrum, the minimum time-bandwidth product, and therefore the shortest pulse, is obtained by a transform-limited pulse, i.e., for a constant spectral phase φ(ω). High values of the time-bandwidth product, on the other hand, indicate a more complex pulse. Pulse shape controlAlthough optical devices also used for continuous light, like beam expanders and spatial filters, may be used for ultrashort pulses, several optical devices have been specifically designed for ultrashort pulses. One of them is the pulse compressor, a device that can be used to control the spectral phase of ultrashort pulses. It is composed of a sequence of prisms, or gratings. When properly adjusted it can alter the spectral phase φ(ω) of the input pulse so that the output pulse is a bandwidth-limited pulse with the shortest possible duration. A pulse shaper can be used to make more complicated alterations on both the phase and the amplitude of ultrashort pulses. To accurately control the pulse, a full characterization of the pulse spectral phase is a must in order to get certain pulse spectral phase (such as Transform-Limited). Then, a Spatial light modulator can be used in the 4f plane to control the pulse. Multiphoton Intrapulse Interference Phase Scan (MIIPS) is a technque based on this concept. Through the phase scan of the spatial light modulator, MIIPS can not only characterize but also manipulate the ultrashort pulse to get the needed pulse shape at target spot (such as transform-limited pulse for optimized peak power, and other sepcific pulse shapes). This technique features with full calibration and control of the ultrashort pulse, with no moving parts, and simple optical setup. Measurement techniquesSeveral techniques are available to measure ultrashort optical pulses:
Methods of characterizing and controlling the ultrashort optical pulses:
Applications of ultrashort pulses
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Ultrashort_pulse". A list of authors is available in Wikipedia. |





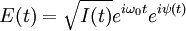
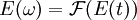
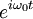 term, E(ω) is centered around ω0, and it is a common practice to refer to E(ω-ω0) by writing just E(ω), which we will do in the rest of this article.
term, E(ω) is centered around ω0, and it is a common practice to refer to E(ω-ω0) by writing just E(ω), which we will do in the rest of this article.