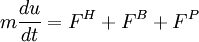Stokesian dynamics

Stokesian Dynamics^[1] is a solution technique for the Langevin equation, which is the relevant form of Newton's 2nd law for a Brownian particle

Additional recommended knowledge

What is the Correct Way to Check Repeatability in Balances?

Weighing the right way

Daily Visual Balance Check

In the above equation F^H is the hydrodynamic force, i.e., force exerted by the fluid on the particle due to relative motion between them. F^B is the stochastic Brownian force due to thermal motion of fluid particles. F^P is the inter particle force,e.g. electrostatic repulsion between like charged particles. Brownian dynamics is one of the popular techniques of solving the Langevin equation. But the hydrodynamic interaction considered in the Brownian dynamics is very naive, normally including only the single body result (isolated particle). On the other hand Stokesian dynamics includes the many body hydrodynamic interaction. Hydrodynamic interaction is very important for non-equilibrium suspensions, like a sheared suspension, where it plays a vital role in its microstructure and hence its properties. So Stokesian dynamics is used primarily for non-equilibrium suspensions and gives excellent agreement with experiments.

Hydrodynamic Interaction

One of the key features of Stokesian Dynamics is its handing of the hydrodynamic interaction, which is fairly accurate without being computationally inhibitive (like Boundary Integral Methods) for a large number of particles. Classical Stokesian dynamics requires O(N³) operation where N is the number of particles in the system (usually a periodic box). Recent advances has brought down the computational cost to O(NlnN)^[2]

References

1. ^ Brady, John; Bossis G. (1988). "Stokesian Dynamics". Ann. Rev. Fluid Mech. 20: 111-157. doi:10.1146/annurev.fl.20.010188.000551.
2. ^ Brady, John; Sierou A. (2001). "Accelerated Stokesian Dynamics simulations". Journal of Fluid Mechanics 448: 115-146.