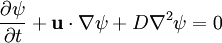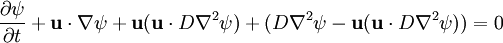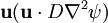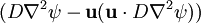To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Streamline diffusionGiven an advection-diffusion equation, streamline diffusion refers to all diffusion going on along the advection direction. Product highlightExplanationIf we take an advection equation, for simplicity of writing we have assumed we may add a diffusion term, again for simplicty, we assume the diffusion to be constant over the entire field.
Giving us an equation on the form: We may now rewrite the equation on the following form: The term below is called streamline diffusion. Crosswind diffusionAny diffusion orthogonal to the streamline diffusion is called crosswind diffusion, for us this becomes the term: Categories: Fluid dynamics | Diffusion |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Streamline_diffusion". A list of authors is available in Wikipedia. |





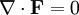 , and
, and 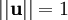
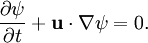
 ,
,