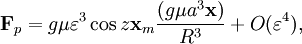The theory of tides is the application of continuum mechanics to interpret and predict the tidal deformations of planetary and satellite bodies and their atmospheres and oceans, under the gravitational loading of another astronomical body or bodies. It commonly refers to the fluid dynamic motions for the Earth's oceans.
Tidal physics
Tidal forcing
The forces discussed here apply to body (Earth tides), oceanic and atmospheric tides. Atmospheric tides on Earth, however, tend to be dominated by forcing due to solar heating.
On the planet (or satellite) experiencing tidal motion consider a point at latitude φ and longitude λ at distance a from the center of mass, then point can written in cartesian coordinates as 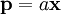 where where
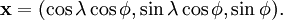
Let δ be the declination and α be the right ascension of the deforming body, the Moon for example, then the vector direction is
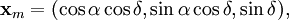
and rm be the orbital distance between the center of masses and Mm the mass of the body. Then the force on the point is
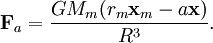
where 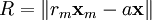 For a circular orbit the angular momentum ω centripetal acceleration balances gravity at the planetary center of mass
For a circular orbit the angular momentum ω centripetal acceleration balances gravity at the planetary center of mass
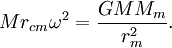
where rcm is the distance between the center of mass for the orbit and planet and M is the planetary mass.
Consider the point in the reference fixed without rotation, but translating at a fixed translation with respect to the center of mass of the planet. The body's centripetal force acts on the point so that the total force is
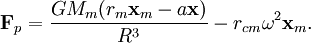
Substituting for center of mass acceleration,
and reordering
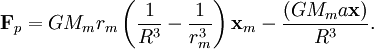
In ocean tidal forcing, the radial force is not significant, the next step is to rewrite the 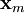 coefficient. Let coefficient. Let 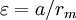 then then
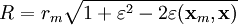
where 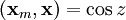 is the inner product determining the angle z of the deforming body or Moon from the zenith. This means that is the inner product determining the angle z of the deforming body or Moon from the zenith. This means that
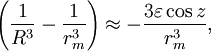
if ε is small. If particle is on the surface of the planet then the local gravity is
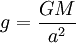 and
set μ = Ma / M. and
set μ = Ma / M.
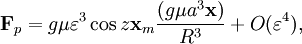
which is a small fraction of g. Note also that force is attractive toward the Moon when the z < π / 2 and repulsive when z > π / 2.
This can also be used to derive a tidal potential.
Laplace tidal equations
-
Laplace summarized the work to his time with a single set of linear partial differential equations simplified from the fluid dynamic equations, but can also be derived via Lagranges equation from energy integrals. It summarizes tidal flow as a barotropic two-dimensional sheet flow, where Coriolis effects are introduced a fictious lateral force.
Thomson rewote Laplace's momentum terms using the curl to find an equation for vorticity. Under certain conditions this can be further rewritten as a conservation of vorticity.
Tidal analysis and prediction
Harmonic analysis
There are about 62 constituents that could be used, but many less are needed to predict tides accurately.
Tidal constituents
Higher harmonics
|
Darwin
|
Period
|
Phase
|
Doodson coefs
|
Doodson
|
Amplitude (cm)
|
NOAA
|
|
Species
|
Symbol
|
(hr)
|
rate(°/hr)
| n1 (L)
| n2 (m)
| n3 (y)
| n4 (mp)
|
number
|
ME
|
MS
|
PR
|
AK
|
CA
|
HI
|
order
|
| Shallow water overtides of principal lunar
| M4
| 6.210300601
| 57.9682084
| 4
|
|
|
| 455.555
| 6.0
| 0.6
|
| 0.9
| 2.3
|
| 5
|
| Shallow water overtides of principal lunar
| M6
| 4.140200401
| 86.9523127
| 6
|
|
|
| 655.555
| 5.1
| 0.1
|
| 1.0
|
|
| 7
|
| Shallow water terdiurnal
| MK3
| 8.177140247
| 44.0251729
| 3
| 1
|
|
| 365.555
|
|
|
| 0.5
| 1.9
|
| 8
|
| Shallow water overtides of principal solar
| S4
| 6
| 60
| 4
| 4
| -4
|
| 491.555
|
| 0.1
|
|
|
|
| 9
|
| Shallow water quarter diurnal
| MN4
| 6.269173724
| 57.4238337
| 4
| -1
|
| 1
| 445.655
| 2.3
|
|
| 0.3
| 0.9
|
| 10
|
| Shallow water overtides of principal solar
| S6
| 4
| 90
| 6
| 6
| -6
|
| *
|
| 0.1
|
|
|
|
| 12
|
| Lunar terdiurnal
| M3
| 8.280400802
| 43.4761563
| 3
|
|
|
| 355.555
|
|
|
|
| 0.5
|
| 32
|
| Shallow water terdiurnal
| 2"MK3
| 8.38630265
| 42.9271398
| 3
| -1
|
|
| 345.555
| 0.5
|
|
| 0.5
| 1.4
|
| 34
|
| Shallow water eighth diurnal
| M8
| 3.105150301
| 115.9364166
| 8
|
|
|
| 855.555
| 0.5
| 0.1
|
|
|
|
| 36
|
| Shallow water quarter diurnal
| MS4
| 6.103339275
| 58.9841042
| 4
| 2
| -2
|
| 473.555
| 1.8
|
|
| 0.6
| 1.0
|
| 37
|
Semi-diurnal
|
Darwin
|
Period
|
Phase
|
Doodson coefs
|
Doodson
|
Amplitude (cm)
|
NOAA
|
| Species
|
Symbol
|
(hr)
|
(°/hr)
| n1 (L)
| n2 (m)
| n3 (y)
| n4 (mp)
|
number
|
ME
|
MS
|
PR
|
AK
|
CA
|
HI
|
order
|
| Principal lunar semidiurnal
| M2
| 12.4206012
| 28.9841042
| 2
|
|
|
| 255.555
| 268.7
| 3.9
| 15.9
| 97.3
| 58.0
| 23.0
| 1
|
| Principal solar semidiurnal
| S2
| 12
| 30
| 2
| 2
| -2
|
| 273.555
| 42.0
| 3.3
| 2.1
| 32.5
| 13.7
| 9.2
| 2
|
| Larger lunar elliptic semidiurnal
| N2
| 12.65834751
| 28.4397295
| 2
| -1
|
| 1
| 245.655
| 54.3
| 1.1
| 3.7
| 20.1
| 12.3
| 4.4
| 3
|
| Larger lunar evectional
| ν2
| 12.62600509
| 28.5125831
| 2
| -1
| 2
| -1
| 247.455
| 12.6
| 0.2
| 0.8
| 3.9
| 2.6
| 0.9
| 11
|
| Variational
| MU2
| 12.8717576
| 27.9682084
| 2
| -2
| 2
|
| 237.555
| 2.0
| 0.1
| 0.5
| 2.2
| 0.7
| 0.8
| 13
|
| Lunar elliptical semidiurnal second-order
| 2"N2
| 12.90537297
| 27.8953548
| 2
| -2
|
| 2
| 235.755
| 6.5
| 0.1
| 0.5
| 2.4
| 1.4
| 0.6
| 14
|
| Smaller lunar evectional
| λ2
| 12.22177348
| 29.4556253
| 2
| 1
| -2
| 1
| 263.655
| 5.3
|
| 0.1
| 0.7
| 0.6
| 0.2
| 16
|
| Larger solar elliptic
| T2
| 12.01644934
| 29.9589333
| 2
| 2
| -3
|
| 272.555
| 3.7
| 0.2
| 0.1
| 1.9
| 0.9
| 0.6
| 27
|
| Smaller solar elliptic
| R2
| 11.98359564
| 30.0410667
| 2
| 2
| -1
|
| 274.555
| 0.9
|
|
| 0.2
| 0.1
| 0.1
| 28
|
| Shallow water semidiurnal
| 2SM2
| 11.60695157
| 31.0158958
| 2
| 4
| -4
|
| 291.555
| 0.5
|
|
|
|
|
| 31
|
| Smaller lunar elliptic semidiurnal
| L2
| 12.19162085
| 29.5284789
| 2
| 1
|
| -1
| 265.455
| 13.5
| 0.1
| 0.5
| 2.4
| 1.6
| 0.5
| 33
|
| Lunisolar semidiurnal
| K2
| 11.96723606
| 30.0821373
| 2
| 2
|
|
| 275.555
| 11.6
| 0.9
| 0.6
| 9.0
| 4.0
| 2.8
| 35
|
Diurnal
|
Darwin
|
Period
|
Phase
|
Doodson coefs
|
Doodson
|
Amplitude (cm)
|
NOAA
|
| Species
|
Symbol
|
(hr)
|
(°/hr)
| n1 (L)
| n2 (m)
| n3 (y)
| n4 (mp)
|
number
|
ME
|
MS
|
PR
|
AK
|
CA
|
HI
|
order
|
| Lunar diurnal
| K1
| 23.93447213
| 15.0410686
| 1
| 1
|
|
| 165.555
| 15.6
| 16.2
| 9.0
| 39.8
| 36.8
| 16.7
| '4
|
| Lunar diurnal
| O1
| 25.81933871
| 13.9430356
| 1
| -1
|
|
| 145.555
| 11.9
| 16.9
| 7.7
| 25.9
| 23.0
| 9.2
| 6
|
| Lunar diurnal
| OO1
| 22.30608083
| 16.1391017
| 1
| 3
|
|
| 185.555
| 0.5
| 0.7
| 0.4
| 1.2
| 1.1
| 0.7
| 15
|
| Solar diurnal
| S1
| 24
| 15
| 1
| 1
| -1
|
| 164.555
| 1.0
|
| 0.5
| 1.2
| 0.7
| 0.3
| 17
|
| Smaller lunar elliptic diurnal
| M1
| 24.84120241
| 14.4920521
| 1
|
|
|
| 155.555
| 0.6
| 1.2
| 0.5
| 1.4
| 1.1
| 0.5
| 18
|
| Smaller lunar elliptic diurnal
| J1
| 23.09848146
| 15.5854433
| 1
| 2
|
| -1
| 175.455
| 0.9
| 1.3
| 0.6
| 2.3
| 1.9
| 1.1
| 19
|
| Larger lunar evectional diurnal
| ρ
| 26.72305326
| 13.4715145
| 1
| -2
| 2
| -1
| 137.455
| 0.3
| 0.6
| 0.3
| 0.9
| 0.9
| 0.3
| 25
|
| Larger lunar elliptic diurnal
| Q1
| 26.868350
| 13.3986609
| 1
| -2
|
| 1
| 135.655
| 2.0
| 3.3
| 1.4
| 4.7
| 4.0
| 1.6
| 26
|
| Larger elliptic diurnal
| 2Q1
| 28.00621204
| 12.8542862
| 1
| -3
|
| 2
| 125.755
| 0.3
| 0.4
| 0.2
| 0.7
| 0.4
| 0.2
| 29
|
| Solar diurnal
| P1
| 24.06588766
| 14.9589314
| 1
| 1
| -2
|
| 163.555
| 5.2
| 5.4
| 2.9
| 12.6
| 11.6
| 5.1
| 30
|
Long period
|
Darwin
|
Period
|
Phase
|
Doodson coefs
|
Doodson
|
Amplitude (cm)
|
NOAA
|
| Species
|
Symbol
|
(hr)
|
(°/hr)
| n1 (L)
| n2 (m)
| n3 (y)
| n4 (mp)
|
number
|
ME
|
MS
|
PR
|
AK
|
CA
|
HI
|
order
|
| Lunar monthly
| Mm
| 661.3111655
| 0.5443747
| 0
| 1
|
| -1
| 65.455
|
|
| 0.7
| 1.9
|
|
| 20
|
| Solar semiannual
| Ssa
| 4383.076325
| 0.0821373
| 0
|
| 2
|
| 57.555
| 1.6
|
| 2.1
| 1.5
| 3.9
|
| 21
|
| Solar annual
| Sa
| 8766.15265
| 0.0410686
| 0
|
| 1
|
| 56.555
|
|
| 5.5
| 7.8
| 3.8
| 4.3
| 22
|
| Lunisolar synodic fortnightly
| Msf
| 354.3670666
| 1.0158958
| 0
| 2
| -2
|
| 73.555
|
|
|
| 1.5
|
|
| 23
|
| Lunisolar fortnightly
| Mf
| 327.8599387
| 1.0980331
| 0
| 2
|
|
| 75.555
|
|
| 1.4
| 2.0
|
| 0.7
| 24
|
Example amplitudes from Eastport, ME; Biloxi, MS; San Juan, PR; Kodiak, AK; San Francisco, CA; and Hilo HI;.
|





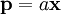 where
where
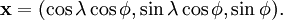
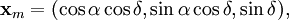
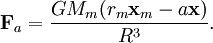
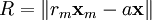 For a circular orbit the angular momentum
For a circular orbit the angular momentum 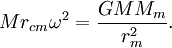
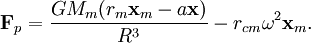
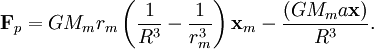
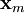 coefficient. Let
coefficient. Let 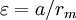 then
then
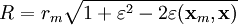
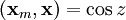 is the inner product determining the angle z of the deforming body or Moon from the zenith. This means that
is the inner product determining the angle z of the deforming body or Moon from the zenith. This means that
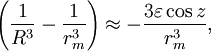
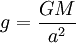 and
set
and
set