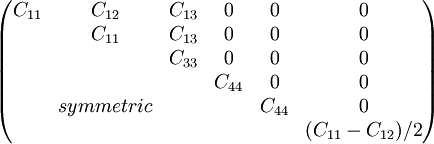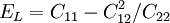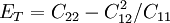Transverse isotropy

A transversely isotropic material is symmetric about an axis that is normal to a plane of isotropy. This transverse plane has infinite planes of symmetry and thus, within this plane, the material properties are same in all directions. With this type of material symmetry, the number of independent constants in the elasticity tensor are reduced to 5 from a total of 21 independent constants in case of fully anisotropic solid. This can be shown by performing transformations involving any rotation about the x3 axis as shown in the figure at left and enforcing no change in the elastic constants. An example of a transversely isotropic material is the so-called on-axis unidirectional fiber composite lamina where the fibers are circular in cross section.In a unidrectional composite, the plane normal to fiber direction can be considered isotropic. In the figure at left, the fibers would be aligned with the x3 axis, and their circular cross section are shown in the figure at right.

Additional recommended knowledge

Better weighing performance in 6 easy steps

What is the Correct Way to Check Repeatability in Balances?

Don't let static charges disrupt your weighing accuracy

The elasticity tensor C_ij has 5 independent constants, which are related to well known engineering elastic moduli in the following way. These engineering moduli are experimentally determined.

Longitudinal Elastic Modulus,

Transverse Elastic Modulus,

Inplane Shear Modulus, G_LT = C₆₆

Poisson's ratio, Nu_LT = C₁₁ / C₂₂

Here, L represents the longitudinal direction and T represents the transverse direction; 1 is the fiber direction.