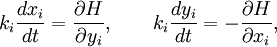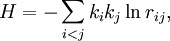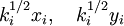Two-dimensional point vortex gas

The two-dimensional point vortex gas is a discrete particle model used to study turbulence in two-dimensional ideal fluids. The two-dimensional guiding-center plasma is a completely equivalent model used in plasma physics.

Additional recommended knowledge

Daily Sensitivity Test

Daily Visual Balance Check

General setup

The model is a Hamiltonian system of N points in the two-dimensional plane executing the motion

$k_i\frac{dx_i}{dt} = \frac{\partial H}{\partial y_i},\qquad k_i\frac{dy_i}{dt} = -\frac{\partial H}{\partial x_i},$

where the k_i are constant and

$H = -\sum_{i<j}k_ik_j \ln r_{ij},\,$

where r_ij is the distance between the ith and jth points.^[1]

The x_i and y_i are not quite canonically conjugate quantities, due to the k_i in the equations of motion. The conjugate quantities are instead

$k_i^{1/2}x_i,\quad k_i^{1/2}y_i$

(In the confined version of the problem, the logarithmic potential is modified.)

Interpretations

In the point-vortex gas interpretation, the particles represent either point vortices in a two-dimensional fluid, or parallel line vortices in a three-dimensional fluid. The constant k_i is the circulation of the fluid around the ith vortex. The Hamiltonian H is the interaction term of the fluid's integrated kinetic energy; it may be either positive or negative. The equations of motion simply reflect the drift of each vortex's position in the velocity field of the other vortices.

In the guiding-center plasma interpretation, the particles represent long filaments of charge parallel to some external magnetic field. The constant k_i is the linear charge density of the ith filament. The Hamiltonian H is just the two-dimensional Coulomb potential between lines. The equations of motion reflect the guiding center drift of the charge filaments, hence the name.

Notes

^ Eyink and Sreenivasan p.90; scaling constants have been omitted

References

Eyink, Gregory and Katepalli Sreenivasan (January 2006). "Onsager and the theory of hydrodynamic turbulence". Reviews of Modern Physics 78: 87-135. doi:10.1103/RevModPhys.78.87.

Categories: Turbulence models | Plasma physics