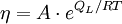To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Viscosity of amorphous materialsViscous flow in amorphous materials (e.g. in glasses and melts) [1][2][3] is a thermally activated process: Product highlight
where Q is activation energy of viscosity, T is temperature, R is the molar gas constant and A is approximately a constant. The viscous flow in amorphous materials is characterised by a deviation from the Arrhenius-type behaviour: Q changes from a high value QH at low temperatures (in the glassy state) to a low value QL at high temperatures (in the liquid state). Depending on this change, amorphous materials are classified as either
The fragility of amorphous materials is numerically characterized by the Doremus’ fragility ratio: RD = QH / QL and strong material have
The viscosity of amorphous materials is quite exactly described by a two-exponential equation:
with constants A1,A2,B,C and D related to thermodynamic parameters of joining bonds of an amorphous material. Not very far from the glass transition temperature, Tg, this equation can be approximated by a Vogel-Tammann-Fulcher (VTF) equation or a Kohlrausch-type stretched-exponential law. If the temperature is significantly lower than the glass transition temperature,
with: QH = Hd + Hm where Hd is the enthalpy of formation of broken bonds (termed configurons) and Hm is the enthalpy of their motion. When the temperature is less than the glass transition temperature, T < Tg, the activation energy of viscosity is high because the amorphous materials are in the glassy state and most of their joining bonds are intact. If the temperature is highly above the glass transition temperature,
with: QL = Hm When the temperature is higher than the glass transition temperature, T > Tg, the activation energy of viscosity is low because amorphous materials are melt and have most of their joining bonds broken which facilitates flow. An example of glass viscosity is given in Calculation of glass properties, in which the viscosity is around 1012 Pa·s at 400°C. References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Viscosity_of_amorphous_materials". A list of authors is available in Wikipedia. |





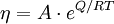
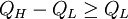
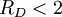 whereas fragile materials have
whereas fragile materials have 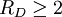
![\eta = A_1 \cdot T \cdot [1 + A_2 \cdot e^{B/RT}] \cdot [1 + C \cdot e^{D/RT}]](images/math/2/c/3/2c36bb3609cd14e755de5a6c44a5d96f.png)
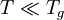 , then the two-exponential equation simplifies to an Arrhenius type equation:
, then the two-exponential equation simplifies to an Arrhenius type equation:
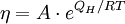
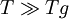 , the two-exponential equation also simplifies to an Arrhenius type equation:
, the two-exponential equation also simplifies to an Arrhenius type equation: