To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Wagner modelWagner model is a rheological model developed for the prediction of the viscoelastic properties of polymers. It might be considered as a simplified practical form of the Bernstein-Kearsley-Zapas model. The model was developed by German rheologist Manfred Wagner. Product highlightFor the isothermal conditions the model can be written as: where:
The strain damping function is usually written as:
The strain hardening function equal to one, then the deformation is small and approaching zero, then the deformations are large. The Wagner equation can be used in the non-isothermal cases by applying time-temperature shift factor. References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Wagner_model". A list of authors is available in Wikipedia. |





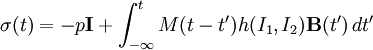
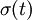 is the
is the 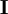 is the unity tensor
is the unity tensor
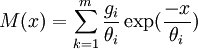 , where for each mode of the relaxation,
, where for each mode of the relaxation, 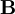 .
.
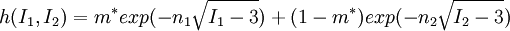 ,
,


