To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Yang–Baxter equationThe Yang–Baxter equation is an equation which was first introduced in the field of statistical mechanics. It takes its name from independent work of C. N. Yang from 1968, and R. J. Baxter from 1982. Product highlight
Parameter-dependent Yang-Baxter equationLet A be a unital associative algebra. The parameter-dependent Yang–Baxter equation is an equation for R(u), a parameter-dependent invertible element of the tensor product for all values of u and v, in the case of an additive parameter, and for all values of u and v, in the case of a multiplicative parameter, where R12(w) = φ12(R(w)), R13(w) = φ13(R(w)), and R23(w) = φ23(R(w)), for all values of the parameter w, and
Parameter-independent Yang–Baxter equationLet A be a unital associative algebra. The parameter-independent Yang–Baxter equation is an equation for R, an invertible element of the tensor product where R12 = φ12(R), R13 = φ13(R), and R23 = φ23(R). Let V be a module of A. Let See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Yang–Baxter_equation". A list of authors is available in Wikipedia. |





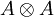 (here,
(here, 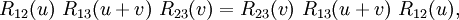
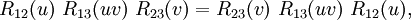
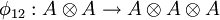 ,
, 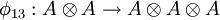 , and
, and 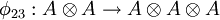 , are algebra morphisms determined by
, are algebra morphisms determined by
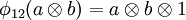 ,
,
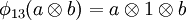 ,
,
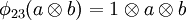 .
.
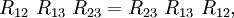
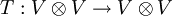 be the linear map satisfying
be the linear map satisfying 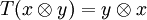 for all
for all 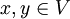 , then a representation of the braid group,
, then a representation of the braid group, 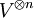 by
by 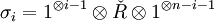 for
for 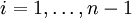 , where
, where 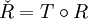 on
on 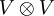 . This representation can be used to determine quasi-invariants of braids, knots and links.
. This representation can be used to determine quasi-invariants of braids, knots and links.


