To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Zeroth law of thermodynamics
The zeroth law of thermodynamics is a generalized statement about bodies in contact at thermal equilibrium and is the basis for the concept of temperature. The most common enunciation of the zeroth law of thermodynamics is:
In other words, the zeroth law says that if considered a mathematical binary relation, thermal equilibrium is transitive. Product highlight
HistoryThe term zeroth law was coined by Ralph H. Fowler. In many ways, the law is more fundamental than any of the others. However, the need to state it explicitly as a law was not perceived until the first third of the 20th century, long after the first three laws were already widely in use and named as such, hence the zero numbering. There is still some discussion about its status in relation to the other three laws. OverviewA system in thermal equilibrium is a system whose macroscopic properties (like pressure, temperature, volume, etc.) are not changing in time. A hot cup of coffee sitting on a kitchen table is not at equilibrium with its surroundings because it is cooling off and decreasing in temperature. Once its temperature stops decreasing, it will be at room temperature, and it will be in thermal equilibrium with its surroundings. Two systems are said to be in thermal equilibrium when 1) both of the systems are in a state of equilibrium, and 2) they remain so when they are brought into contact, where 'contact' is meant to imply the possibility of exchanging heat, but not work or particles. And more generally, two systems can be in thermal equilibrium without thermal contact if one can be certain that if they were thermally connected, their properties would not change in time. Thus, thermal equilibrium is a relation between thermodynamical systems. Mathematically, the zeroth law expresses that this relation is an equivalence relation. (Technically, we would need to also include the condition that a system is in thermal equilibrium with itself.) Equilibrium Between Many SystemsA simple example illustrates why the zeroth law is necessary to complete the equilibrium description. As stated previously, a pair of systems are in equilibrium if small exchanges (e.g., microscopic fluctuations, which are always present) in extensive quantities between them do not lead to a net change in the total energy of both systems (which would be unrecoverable if the energy were reduced). For simplicity, consider N systems in adiabatic isolation from the rest of the universe, both of which have a constant volume and composition, and can only exchange heat (entropy) with one another. (The results of this simple example have a straightforward extension to exchanges in volume or mass.) The combined first and second laws relate the fluctations in total energy δU to the temperature of the ith system Ti and the entropy fluctuation in the ith system δSi by,
The adiabatic isolation of the system from the remaining universe requires that the total sum of the entropy fluctuations vanishes,
that is, entropy can only be exchanged between the N systems. This constraint can be used to re-arrange the expression for the total energy fluctuation to give,
where Tj is the temperature of any system j we may choose to single out among the N systems. Finally, equilibrium requires the total fluctuation in energy to vanish, so we arrive at,
which can be thought of as the vanishing of the product of an anti-symmetric matrix Ti − Tj and a vector of entropy fluctuations δSi. In order for a non-trivial solution to exist,
the determinant of the matrix formed by Ti − Tj must vanish for all choices of j. However, according to Jacobi's theorem, the determinant of an NxN anti-symmetric matrix is always zero if N is odd, although for N even we find that all of the entries must vanish, Ti − Tj = 0, in order to obtain a vanishing determinant, and hence Ti = Tj at equilibrium. This non-intuitive result means that an odd number of systems are always in equilibrium regardless of their temperatures and entropy fluctuations, while equality of temperatures is only required between an even number of systems to achieve equilibrium in the presence of entropy fluctuations. The zeroth law solves this odd vs. even paradox, because it can readily be used to reduce an odd-numbered system to an even number by considering any three of the N systems and eliminating one by application of its principle, and hence reduce the problem to even N which subsequently leads to the same equilibrium condition that we expect in every case, i.e., Ti = Tj. The same result applies to fluctations in any extensive quantity, such as volume (yielding the equal pressure condition), or fluctuations in mass (leading to equality of chemical potentials), and therefore the zeroth law carries implications for a great deal more than just temperature alone. In general, we see that the zeroth law breaks a certain kind of anti-symmetry which still persists in the first and second laws. Temperature and the zeroth lawIt is often claimed, for instance by Max Planck in his influential textbook on thermodynamics, that this law proves that we can define a temperature function, or more informally, that we can 'construct a thermometer'. Whether this is true is a subject in the philosophy of thermal and statistical physics. In the space of thermodynamic parameters, zones of constant temperature will form a surface, which provides a natural order of nearby surfaces. It is then simple to construct a global temperature function that provides a continuous ordering of states. Note that the dimensionality of a surface of constant temperature is one less than the number of thermodynamic parameters (thus, for an ideal gas described with 3 thermodynamic parameter P, V and n, they are 2D surfaces). The temperature so defined may indeed not look like the Celsius temperature scale, but it is a temperature function. For example, if two systems of ideal gas are in equilibrium, then P1V1/N1 = P2V2/N2 where Pi is the pressure in the ith system, Vi is the volume, and Ni is the 'amount' (in moles, or simply number of atoms) of gas. The surface PV / N = const defines surfaces of equal temperature, and the obvious (but not only) way to label them is to define T so that PV / N = RT where R is some constant. These systems can now be used as a thermometer to calibrate other systems. References
|
|||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Zeroth_law_of_thermodynamics". A list of authors is available in Wikipedia. |





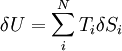 .
.
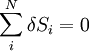 ,
,
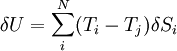 ,
,
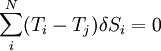 ,
,
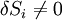 ,
,


