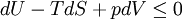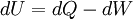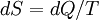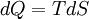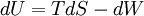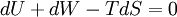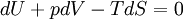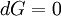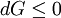Combined law of thermodynamics

In thermodynamics, the combined law of thermodynamics is a mathematical summation of the first law of thermodynamics and the second law of thermodynamics subsumed into a single concise mathematical statement as shown below:

Additional recommended knowledge

Guide to balance cleaning: 8 simple steps

How to quickly check pipettes?

How to ensure accurate weighing results every day?

Here, U is internal energy, T is temperature, S is entropy, p is pressure, and V is volume. In theoretical structure in addition to the obvious inclusion of the first two laws, the combined law incorporates the implications of the zeroth law, via temperature T, and the third law, through its use of free energy as related to the calculation of chemical affinities near absolute zero.

Derivation

Starting from the first law, and neglecting differential details:

From the second law we have:

Hence:

By substituting this into the first law, we have:

Rearranging we have:

Letting dW be pressure-volume work, we have:

By assigning the quantity to the left of the equals sign the symbol G, as Willard Gibbs did in 1876, this reduces to the following at thermodynamic equilibrium:

Or for a spontaneous process:

Thus, this expression is referred to by many as the combined law of thermodynamics; Gibbs showed that deviations of this quantity could be used to predict the direction of various natural chemical processes.