L'énigme de la forme d'un cristal enfin résolue
La méthode permet de prédire la forme des cristaux qui ne sont pas symétriques.
La forme d'un cristal est déterminée par sa chimie intrinsèque, une caractéristique qui détermine finalement sa forme finale à partir des détails les plus élémentaires. Mais parfois, l'absence de symétrie dans un cristal rend les énergies de surface de ses facettes inconnues, ce qui rend difficile toute prédiction théorique de sa forme.

Image symbolique
Computer-generated image
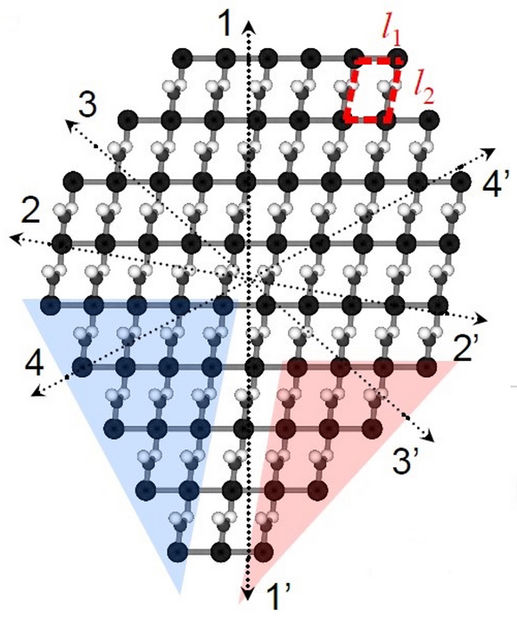
Des chercheurs de l'université Rice ont mis au point une méthode permettant de prédire comment les cristaux prennent forme à partir de leur chimie interne, même lorsque le cristal n'est pas symétrique. Cette représentation d'un cristal de nitrate d'argent comporte huit arêtes, dont aucune ne correspond aux autres. L'algorithme de l'équipe de Rice a tout de même réussi à prédire sa forme.
Illustration by Luqing Wang/Rice University

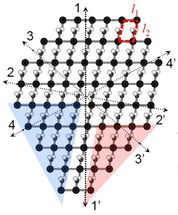
Des théoriciens de l'université Rice affirment avoir trouvé un moyen de contourner cette énigme en attribuant des énergies latentes arbitraires à ses surfaces ou, dans le cas de matériaux bidimensionnels, à ses bords.
Oui, cela ressemble à de la triche, mais de la même manière qu'un magicien trouve une carte de choix dans un jeu en réduisant les possibilités, un petit tour de passe-passe algébrique permet de résoudre le problème de la prédiction de la forme d'un cristal.
La méthode décrite dans Nature Computational Science montre que l'utilisation de ce qu'ils appellent les énergies auxiliaires des bords peut ramener les prédictions en ligne avec la construction de Wulff, une recette géométrique utilisée depuis plus d'un siècle pour déterminer comment les cristaux arrivent à leur forme finale d'équilibre.
L'article en accès libre du physicien des matériaux Boris Yakobson, de l'auteur principal et ancien élève Luqing Wang et de leurs collègues de la George R. Brown School of Engineering de Rice présente des algorithmes qui emploient des nombres arbitraires pour les facteurs de droite dans les équations et fournissent toujours la solution de forme unique appropriée.
"La question de la forme est fascinante, mais les chercheurs ont essayé et échoué pendant des années à calculer les énergies de surface pour les cristaux asymétriques", a déclaré Yakobson. "Il s'avère que nous tombions dans un terrier de lapin, mais nous savions que si la nature peut trouver une solution par le biais d'un gazillion de mouvements atomiques, il devrait également y avoir un moyen pour nous de la déterminer."
Selon lui, le regain d'intérêt pour les matériaux 2D ces derniers temps a motivé cette nouvelle étude. "Nous avons eu un moment 'eurêka' : Après avoir changé notre pensée géométrique en pensée algébrique, nous avons ajouté des équations de fermeture qui contiennent des paramètres arbitraires", a déclaré Yakobson. "Celles-ci semblent inutiles, mais nous avons fait passer le tout dans l'ordinateur et avons observé qu'une forme bien définie en sortait", a-t-il ajouté.
"La partie la plus difficile a été de convaincre nos examinateurs que l'énergie de bord est vraiment indéfinissable, mais qu'une solution peut quand même être obtenue", a déclaré Wang.
Ces travaux pourraient constituer un outil précieux pour les chercheurs qui font croître des cristaux de bas en haut pour des applications catalytiques, lumineuses, sensorielles, magnétiques et plasmoniques, en particulier lorsque leurs formes et leurs bords actifs revêtent une importance particulière.
Les chercheurs ont souligné que les cristaux naturels bénéficient du luxe du temps géologique. Ils parviennent à leurs formes en "réalisant sans relâche une expérience d'essais et d'erreurs" car ils recherchent l'équilibre, c'est-à-dire l'énergie minimale de tous leurs atomes constitutifs.
Mais les approches informatiques et théoriques ne peuvent tout simplement pas traiter des milliards d'atomes à la fois, si bien qu'elles s'appuient généralement sur les énergies des atomes orientés vers l'extérieur. Pour de nombreux cristaux qui ont des facettes ou des bords équivalents, cela fonctionne très bien.
Dans les matériaux 2D, pratiquement tous les atomes sont "tournés vers l'extérieur". Lorsque leurs bords sont équivalents par symétrie - dans les rectangles, par exemple - compléter une construction de Wulff est simple après avoir calculé les énergies des bords via la théorie fonctionnelle de la densité.
Mais en l'absence de symétrie, lorsque tous les bords sont différents, l'énergie moyenne calculée n'a aucun sens, a expliqué M. Yakobson.
"La nature a la réponse pour former un cristal, indépendamment de ce qu'elle sait ou ne sait pas sur les énergies des bords", a-t-il déclaré. "Il existe donc une réponse. Notre défi était de l'imiter avec la théorie."
La première étape vers une solution a été de renoncer consciemment à trouver les énergies absolues des bords, inconnues, et de s'occuper plutôt de leurs combinaisons calculables bien définies, a déclaré Yakobson. D'un point de vue géométrique, c'était une véritable énigme, et pour les matériaux asymétriques en vrac, c'était désespérément compliqué.
"Mais les matériaux en 2D et leurs polygones plans ont rendu la résolution du problème plus facile à envisager que de devoir traiter avec des polyèdres à multiples facettes", a-t-il déclaré.
Trouver et établir les énergies moyennes n'était que la première étape, suivie des "équations de fermeture" qui utilisaient une énergie latente arbitraire du matériau pour le côté droit de l'équation. Même si ces derniers chiffres étaient intentionnellement incorrects, leur application à la construction de Wulff du manuel a permis d'obtenir la forme correcte du cristal.
Le groupe a testé sa théorie sur plusieurs cristaux 2D et a comparé les résultats aux formes finales observées des cristaux. Leurs équations polyvalentes ont permis de prédire les formes, démontrées expérimentalement, du rectangle tronqué formé par le séléniure d'étain 2D, un matériau thermo et piézoélectrique prometteur, et des aiguilles asymétriques formées par le nitrite d'argent.
Note: Cet article a été traduit à l'aide d'un système informatique sans intervention humaine. LUMITOS propose ces traductions automatiques pour présenter un plus large éventail d'actualités. Comme cet article a été traduit avec traduction automatique, il est possible qu'il contienne des erreurs de vocabulaire, de syntaxe ou de grammaire. L'article original dans Anglais peut être trouvé ici.