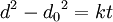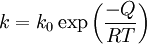Grain growth

Grain growth refers to the increase in size of grains (crystallites) in a material at high temperature. This occurs when recovery and recrystallisation are complete and further reduction in the internal energy can only be achieved by reducing the total area of grain boundary. The term is commonly used in metallurgy but is also used in reference to ceramics and minerals.

Additional recommended knowledge

Safe Weighing Range Ensures Accurate Results

Weighing the right way

How to quickly check pipettes?

Importance of grain growth

Most materials exhibit the Hall-Petch effect at room-temperature and so display a higher yield stress when the grain size is reduced. At high temperatures the opposite is true since the open, disordered nature of grain boundaries means that vacancies can diffuse more rapidly down boundaries leading to more rapid Coble creep. Since boundaries are regions of high energy they make excellent sites for the nucleation of precipitates and other second-phases e.g. Mg-Si-Cu phases in some aluminium alloys or martensite platlets in steel. Depending on the second phase in question this may have positive or negative effects.

Rules of grain growth

Grain growth has long been studied primarily by the examination of sectioned, polished and etched samples under the optical microscope. Although such methods enabled the collection of a great deal of empirical evidence, particular with regard to factors such as temperature or composition, the lack of crystallographic information limited the development of an understanding of the fundamental physics. Nevertheless, the following became well-established features of grain growth:

1. Grain growth occurs by the movement of grain boundaries and not by coalesence (i.e. like water droplets)
2. Boundary movement is discontinuous and the direction of motion may change suddenly.
3. One grain may grow into one grain whilst being consumed from the other side
4. The rate of consumption often increases when the grain is nearly consumed
5. A curved boundary typically migrates towards its centre of curvature
6. When grain boundaries in a single phase meet at angles other than 120 degrees, the grain included by the more acute angle will be consumed so that the angles approach 120 degrees.

Normal vs Abnormal

In common with recovery and recrystallisation, growth phenomena can be separated into continuous and discontinuous mechanisms. In the former the microstructure evolves from state A to B (in this case the grains get larger) in a uniform manner. In the latter, the changes occur heterogeneously and specific transformed and untransformed regions may be identified. Discontinuous grain growth is characterised by a subset of grains growing at a high rate and at the expense of their neighours and tends to result in a microstructure dominated by a few very large grains. In order for this to occur the subset of grains must possess some advantage over their competitors such as a high grain boundary energy, locally high grain boundary mobility, favourable texture or lower local second-phase particle density.

Driving force

The boundary between one grain and its neighbour is a defect in the crystal structure and so it is associated with a certain amount of energy. As a result there is a thermodynamic driving force for the total area of boundary to be reduced. If the grain size increases, accompanied by a reduction in the actual number of grains, then the total area of boundary will be reduced.

In comparison to phase transformations the energy available to drive grain growth is very low and so it tends to occur at much slower rates and is easily slowed by particles or solute atoms.

Ideal grain growth

Ideal grain growth is a special case of normal grain growth where boundary motion is driven only by the reduction of the total amount of grain boundary surface energy. Additional contributions to the driving force by e.g. elastic strains or temperature gradients are neglected. If it holds that the rate of growth is proportional to the driving force and that the driving force is proportional to the total amount of grain boundary energy, then it can be shown that the time t required to reach a given grain size is approximated by the equation

where d_0 is the initial grain size d is the final grain size and k is a temperature dependent constant given by an exponential law:

where k_0 is a constant, T is the absolute temperature and Q is the activation energy for boundary mobility. Theoretically, the activation energy for boundary mobility should equal that for self-diffusion but this is often found to not be the case.

In general these equations are found to hold for ultra-high purity materials but rapidly fail when even tiny concentrations of solute are introduced.

Factors hindering growth

If there are additional factors preventing boundary movement, such as Zener pinning by particles, then the grain size may be restricted to a much lower value than might otherwise be expected. This is an important industrial mechanism in preventing the softening of materials at high temperature.

See also

• Recrystallization (metallurgical)
• Recovery