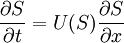To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Buckley–Leverett equationIn fluid dynamics, the Buckley–Leverett equation is a transport equation used to model two-phase flow in porous media. The Buckley–Leverett equation or the Buckley–Leverett displacement can be interpreted as a way of incorporating the microscopic effects to due capillary pressure in two-phase flow into Darcy's law. Product highlightIn a 1D sample (control volume), let S(x,t) be the water saturation, then the Buckley–Leverett equation is where f is the fractional flow rate, Q is the total flow, φ is porosity and A is area of the cross-section in the sample volume. Assumptions for validityThe Buckley–Leverett equation is derived for a 1D sample given
General solutionThe solution of the Buckley–Leverett equation has the form S(x,t) = S(x − U(S)t) which means that U(S) is the front velocity of the fluids at saturation S. See also
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Buckley–Leverett_equation". A list of authors is available in Wikipedia. |