To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Generic scalar transport equationThe generic scalar transport equation is a general partial differential equation that describes transport phenomena such as heat transfer, mass transfer, fluid dynamics (momentum transfer), etc. A general form of the equation is Product highlightwhere f is called the flux, and g is called the source. All the transfer processes express a certain conservation principle. In this respect, any differential equation addresses a certain quantity as its dependent variable and thus expresses the balance between the phenomena affecting the evolution of this quantity. For example, the temperature of a fluid in a heated pipe is affected by convection due to the solid-fluid interface, and due to the fluid-fluid interaction. Furthermore, temperature is also diffused inside the fluid. For a steady-state problem, with the absence of sources, a differential equation governing the temperature will express a balance between convection and diffusion. A brief inspection of the equations governing various transport phenomena reveal that all of these equations can be put into a generic form thus allowing a systematic approach for a computer simulation. For example, the conservation equation of a concentration of a substance ci is where The x-momentum equation for a Newtonian fluid can be written as where Bx is the body force in the x-direction and Vx includes the viscous terms that are not expressed by Upon inspection of the above equations, it can be inferred that all the dependent variables seem to obey a generalized conservation principle. If the dependent variable (scalar or vector) is denoted by φ, the generic differential equation is where Γ is the diffusion coefficient, or diffusivity.
The objective of all discretization techniques (finite difference, finite element, finite volume, boundary element, etc.) is to devise a mathematical formulation to transform each of these terms into an algebraic equation. Once applied to all control volumes in a given mesh, we obtain a full linear system of equations that needs to be solved. Scalar transport equation in financial mathematicsSome equations that governs the dynamics of financial derivatives in financial markets can be also categorized as generic scalar transport equations. Examples include the Black-Scholes equation. See also |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Generic_scalar_transport_equation". A list of authors is available in Wikipedia. |


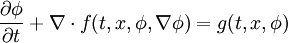



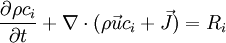
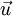 denotes the velocity field,
denotes the velocity field, 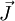 denotes the diffusion flux of the chemical species, and
denotes the diffusion flux of the chemical species, and 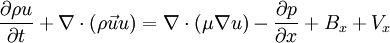
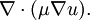
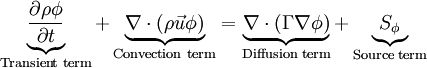
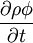 , accounts for the accumulation of
, accounts for the accumulation of 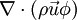 , accounts for the transport of
, accounts for the transport of 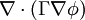 , accounts for the transport of
, accounts for the transport of 

