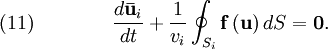To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Finite volume methodThe finite volume method is a method for representing and evaluating partial differential equations as algebraic equations. Similar to the finite difference method, values are calculated at discrete places on a meshed geometry. "Finite volume" refers to the small volume surrounding each node point on a mesh. In the finite volume method, volume integrals in a partial differential equation that contain a divergence term are converted to surface integrals, using the divergence theorem. These terms are then evaluated as fluxes at the surfaces of each finite volume. Because the flux entering a given volume is identical to that leaving the adjacent volume, these methods are conservative. Another advantage of the finite volume method is that it is easily formulated to allow for unstructured meshes. The method is used in many computational fluid dynamics packages. Product highlight
1D exampleConsider a simple 1D advection problem defined by the following partial differential equation Here, and at time where
where We can therefore derive a semi-discrete numerical scheme for the above problem with cell centres indexed as where values for the edge fluxes, General hyperbolic problemWe can also consider a general hyperbolic problem, represented by the following PDE, Here, On integrating the first term to get the volume average and applying the divergence theorem to the second, this yields where Again, values for the edge fluxes can be reconstructed by interpolation or extrapolation of the cell averages. The actual numerical scheme will depend upon problem geometry and mesh construction. MUSCL reconstruction is often used in high resolution schemes where shocks or discontinuities are present in the solution. Finite volume schemes are conservative as cell averages change through the edge fluxes. In other words, one cell's loss is another cell's gain! See also
References |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Finite_volume_method". A list of authors is available in Wikipedia. |





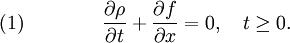
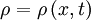 represents the state variable and
represents the state variable and 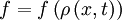 represents the flux or flow of
represents the flux or flow of 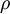 . Conventionally, positive
. Conventionally, positive 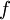 represents flow to the right whilst negative
represents flow to the right whilst negative 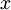 , into finite volumes or cells with cell centres indexed as
, into finite volumes or cells with cell centres indexed as 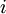 . For a particular cell,
. For a particular cell, 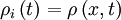 at time
at time 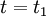 and
and ![{ x \in \left[ x_{i-\frac{1}{2}} , x_{i+\frac{1}{2}} \right] }\](images/math/d/1/d/d1d64cd7d0d48354cc4f2f7150672590.png) , as
, as
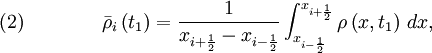
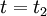 as,
as,
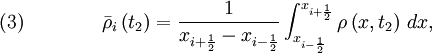
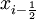 and
and 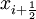 represent locations of the upstream and downstream faces or edges respectively of the
represent locations of the upstream and downstream faces or edges respectively of the 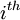 cell.
cell.
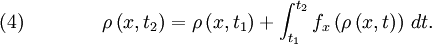
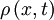 at time
at time 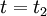 , we integrate
, we integrate 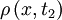 over the cell volume,
over the cell volume, 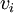 and divide the result by
and divide the result by 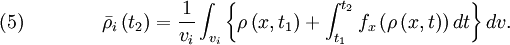
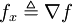 , we can apply the divergence theorem and substitute for the volume integral of the divergence with the values of
, we can apply the divergence theorem and substitute for the volume integral of the divergence with the values of 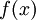 at the cell edges
at the cell edges ![\quad (6) \qquad \qquad \bar{\rho}_i \left( t_2 \right) = \frac{1}{\Delta x_{i}} \left[ \int_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} \rho \left(x,t_1 \right)\, dx + \int_{t_1}^{t_2} f_{i + \frac{1}{2}} dt - \int_{t_1}^{t_2} f_{i - \frac{1}{2}} dt \right] .](images/math/c/3/e/c3e9d46ad2a9d724e872232b11796679.png)
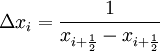 and
and 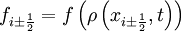 .
.
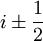 , by differentiating (6) with respect to time to obtain:
, by differentiating (6) with respect to time to obtain:
![\quad (7) \qquad \qquad \frac{d \bar{\rho}_i}{d t} + \frac{1}{\Delta x_i} \left[ f_{i + \frac{1}{2}} - f_{i - \frac{1}{2}} \right] =0 ,](images/math/3/3/2/332850158c60d9cab497cb24e5185509.png)
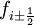 , can be reconstructed by interpolation or extrapolation of the cell averages. It should be noted that equation (7) is exact for the volume averages; i.e., no approximations have been made during its derivation.
, can be reconstructed by interpolation or extrapolation of the cell averages. It should be noted that equation (7) is exact for the volume averages; i.e., no approximations have been made during its derivation.
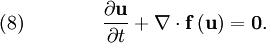
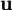 represents a vector of states and
represents a vector of states and 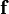 represents the corresponding flux vector. Again we can sub-divide the spatial domain into finite volumes or cells. For a particular cell,
represents the corresponding flux vector. Again we can sub-divide the spatial domain into finite volumes or cells. For a particular cell, 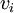 , which gives,
, which gives,
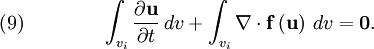
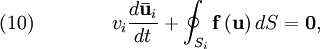
 represents the total surface area of the cell. So, finally, we are able to present the general result equivalent to (7), i.e.
represents the total surface area of the cell. So, finally, we are able to present the general result equivalent to (7), i.e.