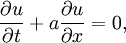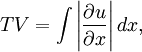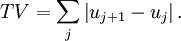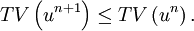Total variation diminishing

In systems described by partial differential equations, such as the following hyperbolic advection equation,

Additional recommended knowledge

Weighing the right way

What is the Sensitivity of my Balance?

Daily Visual Balance Check

the total variation (TV) is given by,

and the total variation for the discrete case is,

A numerical method is said to be total variation diminishing (TVD) if,

A system is said to be monotonicity preserving if the following properties are maintained as a function of t:

• No new local extrema can be created within the solution spatial domain,
• The value of a local minimum is non-decreasing, and the value of a local maximum is non-increasing.

For physically realisable systems where there is energy dissipation of some kind, the total variation does not increase with time. Harten 1986 proved the following properties for a numerical scheme,

• A monotone scheme is TVD, and

• A TVD scheme is monotonicity preserving.

Monotone schemes are attractive for solving engineering and scientific problems because they do not provide non-physical solutions.

Godunov's theorem proves that only first order linear schemes preserve monotonicity and are therefore TVD. Higher order linear schemes, whilst more accurate for smooth solutions, are not TVD and tend to introduce spurious oscillations (wiggles) where discontinuities or shocks arise. To overcome these draw backs, various high-resolution, non-linear techniques have been developed, often using flux/slope limiters.

See also

• Flux limiters
• Godunov's theorem
• High-resolution scheme
• MUSCL scheme
• Sergei K. Godunov
• Total variation

References

• Harten, Ami (1983), " ", J. Comput. Phys 49: 357-393, doi:10.1006/jcph.1997.5713

Further reading

• Hirsch, C. (1990), Numerical Computation of Internal and External Flows, vol 2, Wiley.
• Laney, Culbert B. (1998), Computational Gas Dynamics, Cambridge University Press.
• Toro, E. F. (1999), Riemann Solvers and Numerical Methods for Fluid Dynamics, Springer-Verlag.
• Tannehill, John C., et al, (1997), Computational Fluid mechanics and Heat Transfer, 2nd Ed., Taylor and Francis.
• Wesseling, Pieter (2001), Principles of Computational Fluid Dynamics, Springer-Verlag.