Characteristic state function

The characteristic state function in statistical mechanics refers to a particular relationship between the partition function of an ensemble.

Additional recommended knowledge

Weighing the right way

Safe Weighing Range Ensures Accurate Results

Essential Laboratory Skills Guide

In particular, if the partition function P satisfies

P = exp( − βQ) or P = exp( + βQ)

in which Q is a thermodynamic quantity, then Q is known as the "characteristic state function" of the ensemble corresponding to "P". Beta refers to the thermodynamic beta.

Examples

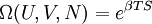• The microcanonical ensemble satisfies hence, its characteristic state function is 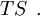This quantity roughly speaking, denotes the energy of the entropy at a particular temperature.

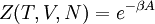• The canonical ensemble satisfies hence, its characteristic state function is the Helmholtz free energy.

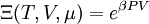• The grand canonical ensemble satisfies , so its characteristic state function is the total Pressure-volume work.

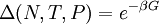• The isothermal-isobaric ensemble satisfies so its characteristic function is the Gibbs free energy.