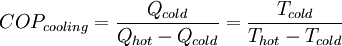To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Coefficient of performanceThe coefficient of performance, or COP (sometimes CP), of a heat pump is the ratio of the output heat to the supplied work or Product highlight
According to the first law of thermodynamics, in a reversible system we can show that Qhot = Qcold + W and W = Qhot − Qcold, where Qhot is the heat taken in by the cold heat reservoir and Qcold is the heat given off by the hot heat reservoir.
Therefore, by substituting for W,
Hence,
COPheating applies to heat pumps and COPcooling applies to air conditioners or refrigerators. For heat engines, see Efficiency. ExampleA geothermal heat pump operating at COPheating 3.5 provides 3.5 units of heat for each unit of energy consumed (e.g. 1 kW consumed would provide 3.5 kW of output heat). The output heat comes from both the heat source and 1 kW of input energy, so the heat-source is cooled by 2.5 kW, not 3.5 kW. A heat pump of COPheating 3.5, such as in the example above, could be less expensive to use than even the most efficient gas furnace. A heat pump cooler operating at COPcooling 2.0 removes 2 units of heat for each unit of energy consumed (e.g. such an air conditioner consuming 1 kW would remove heat from a building's air at a rate of 2 kW). The COP of heat pumps compares favorably with high-efficiency gas-burning furnaces (90-99% efficient), and electric heating (100%), but the full costs of the energy consumed must be considered, and energy from gas is typically much less expensive than that from electricity. See also
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Coefficient_of_performance". A list of authors is available in Wikipedia. |





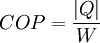 where Q is the useful heat supplied by the condenser and W is the work consumed by the compressor. (Note: COP has no units, therefore in this equation, heat and work must be expressed in the same units.)
where Q is the useful heat supplied by the condenser and W is the work consumed by the compressor. (Note: COP has no units, therefore in this equation, heat and work must be expressed in the same units.)
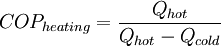 For a heat pump operating at maximum theoretical efficiency (i.e. Carnot efficiency), it can be shown that
For a heat pump operating at maximum theoretical efficiency (i.e. Carnot efficiency), it can be shown that 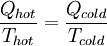 and
and 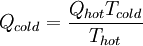 , where
, where 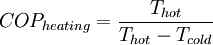 Similarly,
Similarly,