My watch list

Colebrook equation

It has been suggested that this article or section be merged into Frictional pressure drop. (Discuss)

The Colebrook Equation is an implicit equation which combines experimental results of studies of laminar and turbulent flow in pipes. It was developed in 1939 by C. F. Colebrook.

Additional recommended knowledge

Daily Sensitivity Test

How to quickly check pipettes?

Guide to balance cleaning: 8 simple steps

It is defined as:

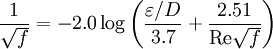
$\frac{1}{\sqrt{f}}=-2.0 \log \left( \frac { \varepsilon/D} {3.7} + \frac {2.51} {\mathrm{Re} \sqrt{f}} \right)$

where:

$f$ is the Darcy friction factor
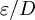$\varepsilon/D$ is the relative roughness
$Re$ is the Reynolds number

Due to the implicit nature of the Colebrook equation, determination of a friction factor requires some iteration or a numerical solving method. Therefore, an approximate explicit relation for $f$ was determined by S. E. Haaland in 1983.

This equation is known as the Haaland equation, and is defined as:

$\frac{1}{\sqrt {f}} = -1.8 \log \left[ \left( \frac{\varepsilon/D}{3.7} \right)^{1.11} + \frac{6.9}{\mathrm{Re}} \right]$