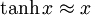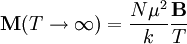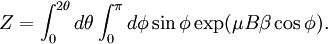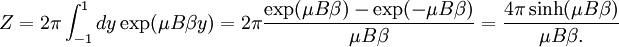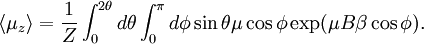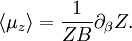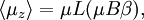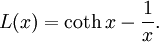To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Curie's lawIn a paramagnetic material Curie's law relates the magnetization of the material to the applied magnetic field and temperature.
This relation was discovered experimentally (by fitting the results to a correctly guessed model) by Pierre Curie. Product highlight
Simple Derivation (Statistical Mechanics)
A simple model of a paramagnet concentrates on the particles which compose it, call them paramagnetons. Assuming that each paramagneton has a magnetic moment given by : To simplify the calculation, we are going to work with a 2-state paramagnet, that is, the particle may either align its magnetic moment with the magnetic field, or against it. No other orientations are possible, μ and − μ. If so, then such a particle has only two possible energies
and
With this information we can construct the partition function of one paramagneton When one seeks the magnetization of a paramagnet, one is interested in the likelihood of a paramagneton to align itself with the field. In other words, one seeks the expectation value of orientation μ. where the probability of a configuration is given by its Boltzmann factor, and the partition function provides the necessary normalization for probabilities (so that the sum of all of them is unity.) A standard procedure is to express this as a derivative with respect to β But now what is differentiated is nothing but the partition function again. As
This is magnetization of one paramagneton, total magnetization of the solid is given by The formula above is known as the Langevin Paramagnetic equation. Pierre Curie found an approximation to this law which applies to the relatively high temperatures and low, magnetic fields used in his experiments. Let's see what happens to the magnetization as we specialize it to large T and small B. As temperature increases and magnetic field decreases, the argument of hyperbolic tangent decreases. Another way to say this is this is sometimes called the Curie regime. We also know that if so Q.E.D. More Involved Derivation (Statistical Mechanics)A more involved treatment applies when the paramagnetons are supposed to rotate freely. In this case, their position will be determined by their angles in spherical coordinates, and the energy for one of them will be:
where φ is the angle between the magnetic moment and the magnetic field (which we take to be pointing in the z coordinate.) The corresponding partition function is We seeing there is no dependence on the θ angle, and we can change variables to y = cosφ to obtain Now, the expected value of the z component of the magnetization (the other two are seen to be null, as the should) will be given by Again, we see this can be written as a differentiation of Z: Carrying out the derivation we find where L is the Langevin function: This function is not singular for small x, since the two singular terms cancel each other. In fact, its behavior for small arguments is the same as the tanh function, so the limit above also applies in this case. ApplicationsIt is the basis of operation of magnetic thermometers, which are used to measure very low temperatures. See also |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Curie's_law". A list of authors is available in Wikipedia. |


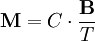
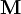 is the resulting magnetisation
is the resulting magnetisation
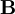 is the magnetic field, measured in
is the magnetic field, measured in 


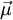 . Energy of a
. Energy of a 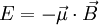
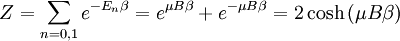
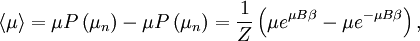
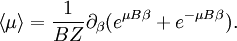
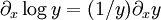 , we can write
, we can write
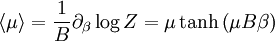
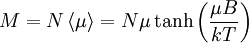
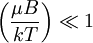
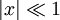 , then
, then