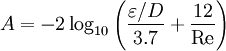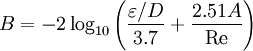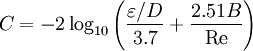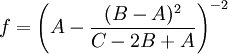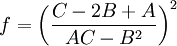To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Darcy friction factor formulaeThis article consolidates various formulae for the Darcy friction factor which are found in several Wikipedia articles. The Darcy friction factor is also known as the Darcy–Weisbach friction factor and is four times larger than the Fanning friction factor. Product highlight
Flow RegimesWhich friction factor formula may be applicable depends upon the type of flow that exists:
Laminar FlowThe Darcy friction factor for laminar flow (Reynolds number less than 2000) is given by the following formula: where:
Transition FlowTransition (neither fully-laminar nor fully-turbulent) flow occurs in the range of Reynolds numbers between 2000 and 4000. The value of the Darcy friction factor may be subject to large uncertainties in this flow regime.
Turbulent Flow in Smooth ConduitsEmpirical correlations exist for this flow regime. Such correlations are included in the ASHRAE Handbook of Fundamentals.
Turbulent Flow in Rough ConduitsThe Darcy friction factor for fully turbulent flow (Reynolds number greater than 4000) in rough conduits is given by the Colebrook equation.
Choosing a FormulaIf more than one formula is applicable in the flow regime under consideration, the choice of formula may be influenced by one or more of the following:
Colebrook EquationThe Colebrook Equation is an implicit equation which combines experimental results of studies of laminar and turbulent flow in pipes. It was developed in 1939 by C. F. Colebrook. It is used to iteratively solve for the Darcy-Weisbach friction factor f. This equation is also known as the Colebrook-White equation. For conduits that are flowing completely full of fluid at Reynolds numbers greater than 4000, it is defined as:
where:
Additional, mathematically-equivalent forms of the Colebrook equation are:
and
The additional equivalent forms above assume that the constants 3.7 and 2.51 in the formula at the top of this section are exact. The constants are probably values which were rounded by Colebrook during his curve fitting; but they are effectively treated as exact when comparing (to several decimal places) results from explicit formulae (such as those found elsewhere in this article) to the friction factor computed via Colebrook's implicit equation. Equations similar to the additional forms above (with the constants rounded to fewer decimal places -- or perhaps shifted slightly to minimize overall rounding errors) may be found in various references. It may helpful to note that they are essentially the same equation.
Haaland equationThe Haaland equation is used to solve directly for the Darcy-Weisbach friction factor f for a full-flowing circular pipe. It is an approximation of the implicit Colebrook-White equation. It was developed by S. E. Haaland in 1983. The Haaland equation is defined as:
where:
Swamee-Jain equationThe Swamee-Jain equation is used to solve directly for the Darcy-Weisbach friction factor f for a full-flowing circular pipe. It is an approximation of the implicit Colebrook-White equation. Where f is a function of:
The equation was found to match the Colebrook-White equation within 1.0% for 10-6 < ε/D < 10-2 and 5000 < Re < 108.
Serghide's solutionSerghide's solution is used to solve directly for the Darcy-Weisbach friction factor f for a full-flowing circular pipe. It is an approximation of the implicit Colebrook-White equation, and is derived by taken an iterative approach to solving the equation, then applying a Shanks transformation[citation needed] to the first three terms of the series. The solution involves calculating three intermediate values and then substituting those values into a final equation. where f is a function of:
The equation was found to match the Colebrook-White equation within 0.0031% for all practical applications. A mathematical equivalent for the last equation is: This form may not be computationally equivalent for some values of (AC - B2) due to rounding errors in computerized calculations. References
Categories: Equations of fluid dynamics | Fluid mechanics |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Darcy_friction_factor_formulae". A list of authors is available in Wikipedia. |





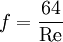
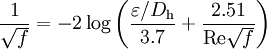
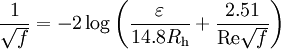
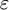 (m, ft)
(m, ft)
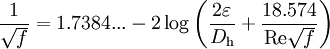
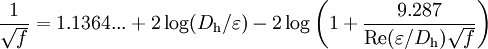
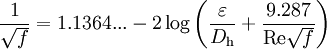
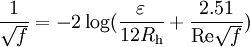
![\frac{1}{\sqrt {f}} = -1.8 \log \left[ \left( \frac{\varepsilon/D}{3.7} \right)^{1.11} + \frac{6.9}{\mathrm{Re}} \right]](images/math/a/a/5/aa588ea7ec602168822b688bdfb1407b.png)
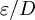 is the relative roughness
is the relative roughness
![f = \frac{0.25}{[log (\frac{\epsilon}{3.7D} + \frac{5.74}{Re^{0.9}})]^2}](images/math/4/7/b/47b1576392bdce0c754aa2c9a9225a2d.png)