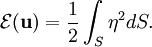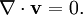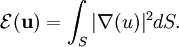To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
EnstrophyIn fluid dynamics, the enstrophy Product highlightHere, since the curl gives a vector field in 2-dimensions (vortex) corresponding to the vector valued velocity component in the Navier-Stokes equations, we can integrate its square over a surface S to retrieve a continuous linear operator, known as a current. This equation is however somewhat misleading. Here we have chosen a simplified version of the enstrophy derived from the incompressibility condition, which reduces to vanishing divergence, More generally, when not restricted to the incompressible condition, the enstrophy may be computed by: The enstrophy can be interpreted as another type of potential density (ie. see probability density); or, more concretely, the equantity directly related to the kinetic energy in the flow model that corresponds to dissipation effects in the fluid. It is particularly useful in the study of turbulent flows, and is often identified in the study of thrusters as well as the field of flame theory.
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Enstrophy". A list of authors is available in Wikipedia. |


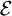 can be described as the integral of the square of the
can be described as the integral of the square of the 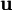 as,
as,