To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Fractional quantum Hall effectThe fractional quantum Hall effect (FQHE) is a fascinating manifestation of simple collective behaviour in a two-dimensional system of strongly interacting electrons. At particular magnetic fields, the electron gas condenses into a remarkable state with liquid-like properties. This state is very delicate, requiring high quality material with a low carrier concentration, and extremely low temperatures. As in the integer quantum Hall effect, a series of plateaus forms in the Hall resistance. Each particular values of magnetic field corresponds to a filling factor (the ratio of electrons to magnetic flux quanta)
Product highlightwhere p and q are integers with no common factors. Here q turns out to be an odd number with the exception of two enigmatic filling factors 5/2 and 7/2. The principal series of such fractions are
and
There are two main theories of the FQHE.
The FQHE was experimentally discovered in 1982 by Daniel Tsui and Horst Störmer, in experiments performed on gallium arsenide heterostructures developed by Arthur Gossard. The effect was explained by Robert B. Laughlin in 1983, using a novel quantum liquid phase that accounts for the effects of interactions between electrons. Tsui, Störmer, and Laughlin were awarded the 1998 Nobel Prize for their work. Although it was generally assumed that the discrete resistivity jumps found in the Tsui experiment were due to the presence of fractional charges (i.e., due to the emergence of quasiparticles with charges smaller than an electron charge), it was not until 1997 that R. de-Picciotto, et al., indirectly observed fractional charges through measurements of quantum shot noise. Fractionally charged quasiparticles are neither bosons nor fermions and exhibit anyonic statistics. The fractional quantum Hall effect continues to be influential in theories about topological order. Certain fractional quantum Hall phases appear to have the right properties for building a topological quantum computer. References
Categories: Hall effect | Condensed matter physics |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Fractional_quantum_Hall_effect". A list of authors is available in Wikipedia. |





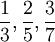 etc.,
etc.,
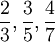 , etc.
, etc.
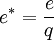 , where the fraction is
, where the fraction is 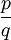 as above.
as above.
 to each electron, forming integer-charged quasiparticles called composite fermions. The fractional states are mapped to the integer
to each electron, forming integer-charged quasiparticles called composite fermions. The fractional states are mapped to the integer 

