To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Quantum Hall effectThe quantum Hall effect (or integer quantum Hall effect) is a quantum-mechanical version of the Hall effect, observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall conductance where Product highlight
ApplicationsThe quantization of the Hall conductance has the important property of being incredibly precise. Actual measurements of the Hall conductance have been found to be integer or fractional multiples of HistoryThe integer quantization of the Hall conductance was originally predicted by Ando, Matsumoto, and Uemura in 1975, on the basis of an approximate calculation. Several workers subsequently observed the effect in experiments carried out on the inversion layer of MOSFETs. It was only in 1980 that Klaus von Klitzing, working with samples developed by Michael Pepper and Gerhard Dorda, made the unexpected discovery that the Hall conductivity was exactly quantized. For this finding, von Klitzing was awarded the 1985 Nobel Prize in Physics. The link between exact quantization and gauge invariance was subsequently found by Robert Laughlin. Most integer quantum Hall experiments are now performed on gallium arsenide heterostructures, although many other semiconductor materials can be used. Integer quantum Hall effect has also been found in graphene at temperatures as high as room temperature. MathematicsThe integers that appear in the Hall effect are examples of topological quantum numbers. They are known in mathematics as the first Chern numbers and are closely related to Berry's phase. A striking model of much interest in this context is the Azbel-Harper-Hofstadter model whose quantum phase diagram is the Hofstadter's butterfly shown in the figure. The vertical axis is the strength of the magnetic field and the horizontal axis is the chemical potential, which fixes the electron density. The colors represent the integer Hall conductances. Warm colors represent positive integers and cold colors negative integers. The phase diagram is fractal and has structure on all scales. See alsoReferences
Categories: Hall effect | Condensed matter physics | Quantum electronics | Spintronics |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Quantum_Hall_effect". A list of authors is available in Wikipedia. |


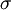 takes on the quantized values
takes on the quantized values
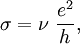
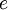 is the elementary charge and
is the elementary charge and 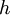 is Planck's constant. In the "ordinary" quantum Hall effect, known as the integer quantum Hall effect,
is Planck's constant. In the "ordinary" quantum Hall effect, known as the integer quantum Hall effect, 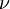 takes on integer values (
takes on integer values ( 


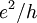 to nearly one part in a billion. This phenomenon, referred to as "exact quantization", has been shown to be a subtle manifestation of the principle of gauge invariance. It has allowed for the definition of a new practical standard for electrical resistance: the resistance unit
to nearly one part in a billion. This phenomenon, referred to as "exact quantization", has been shown to be a subtle manifestation of the principle of gauge invariance. It has allowed for the definition of a new practical standard for electrical resistance: the resistance unit 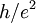 , roughly equal to 25812.8
, roughly equal to 25812.8 

