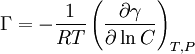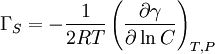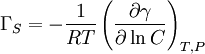My watch list

Gibbs isotherm

Gibbs isotherm is an equation which could be considered an adsorption isotherm that connects surface tension of a solution with the concentration of the solute. Substances can have different effects on surface tension:

No effect, for example sugar
Increase of surface tension, inorganic salts
Decrease surface tension progressively, alcohols
Decrease surface tension and, once a minimum is reached, no more effect: surfactants

Additional recommended knowledge

Weighing the right way

Daily Sensitivity Test

Don't let static charges disrupt your weighing accuracy

Starting from the consideration of thermodynamic equilibrium, Josiah Willard Gibbs proved that surface tension and concentration are linked through surface concentration, $Γ$ , represents excess of solute per unit area of the surface over what would be present if the bulk concentration prevailed all the way to the surface, it can be positive, negative or zero. It has units of mol/m². In the derivation of the equation it is assumed that the solution is ideal, (so $μ = μ o + R T ln C$ ) and surface concentration of the solvent is zero, so it is only valid under these assumptions. It is also considered that the interface is bidimensional, which is not true, further models as Guggenheim's correct this flaw.

Gibbs isotherm is $\Gamma = - \frac{1}{RT} \left( \frac{\partial \gamma}{\partial \ln C} \right)_{T,P}$

C is the concentration of the substance in the bulk solution, R is the gas constant, T the temperature and $γ$ is the surface tension of the solution.

Therefore inorganic salts have negative surface concentrations (which is logical, because they have strong attractions with the solvent) and surfactants have positive surface concentrations: they adsorb on the interface.

A method for determining surface concentrations is needed in order to prove the validity of the model: two different techniques are normally used: elipsometry and following the decay of ¹⁴C present in the surfactant molecules.