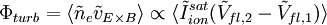To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Langmuir probeA Langmuir probe is a device named after Nobel Prize winning physicist Irving Langmuir, used to determine the electron temperature, electron density, and electric potential of a plasma. It works by inserting one or more electrodes into a plasma, with a constant or time-varying electric potential between the various electrodes or between them and the surrounding vessel. The measured currents and potentials in this system allow the determination of the physical properties of the plasma. Product highlight
I-V characteristic of the Debye sheathThe beginning of Langmuir probe theory is the I-V characteristic of the Debye sheath, that is, the current density flowing to a surface in a plasma as a function of the voltage drop across the sheath. The analysis presented here indicates how the electron temperature, electron density, and plasma potential can be derived from the I-V characteristic. In some situations a more detailed analysis can yield information on the ion density (ni), the ion temperature Ti, or the electron energy distribution function (EEDF) or fe(v). Ion saturation current densityConsider first a surface biased to a large negative voltage. If the voltage is large enough, essentially all electrons (and any negative ions) will be repelled. The ion velocity will satisfy the Bohm sheath criterion, which is, strictly speaking, an inequality, but which is usually marginally fulfilled. The Bohm criterion in its marginal form says that the ion velocity at the sheath edge is simply the sound speed given by
The ion temperature term is often neglected, which is justified if the ions are cold. Even if the ions are known to be warm, the ion temperature is usually not known, so it is usually assumed to be simply equal to the electron temperature. In that case, consideration of finite ion temperature only results in a small numerical factor. Z is the (average) charge state of the ions, and γi is the adiabatic coefficient for the ions. The proper choice of γi is a matter of some contention. Most analyses use γi = 1, corresponding to isothermal ions, but some kinetic theory suggests that γi = 3, corresponding to one degree of freedom, is more appropriate. For Z = 1 and Ti = Te, using the larger value results in the conclusion that the density is The charge density of the ions depends on the charge state Z, but quasineutrality allows one to write it simply in terms of the electron density as ene. Using these results we have the current density to the surface due to the ions. The current density at large negative voltages is due solely to the ions and, except for possible sheath expansion effects, does not depend on the bias voltage, so it is referred to as the ion saturation current density and is given by
where the plasma parameters, in particular the density, are those at the sheath edge. Exponential electron currentAs the potential drop in the Debye sheath is reduced, the more energetic electrons are able to overcome the potential barrier of the electrostatic sheath. We can model the electrons at the sheath edge with a Boltzmann distribution, i.e.,
except that the high energy tail moving away from the surface is missing, because only the lower energy electrons moving toward the surface are reflected. The higher energy electrons overcome the sheath potential and are absorbed. The mean velocity of the electrons which are able to overcome the potential drop of the sheath is
where the cut-off velocity for the upper integral is
Φsh is the potential drop across the Debye sheath, that is, the potential at the sheath edge minus the potential of the surface. For a potential drop large compared to the electron temperature, the result is
With this expression we can write the electron contribution to the current to the probe in terms of the ion saturation current as
valid as long as the electron current is not more than two or three times the ions current. Floating potentialThe total current, of course, is the sum of the ion and electron currents:
We are using the convention that current from the surface into the plasma is positive. An interesting and practical question is the potential of a surface to which no net current flows. It is easily seen from the above equation that
If we introduce the reduced ion mass μi = mi / mp, we can write
Since the floating potential is the experimentally accessible quantity, the current (below electron saturation) is usually written as
Electron saturation currentWhen the electrode potential is equal to or greater than the plasma potential, then there is no longer a sheath to reflect electrons, so we may expect the electron current to saturate. Using the Boltzmann expression for the mean electron velocity given above with ve0 = 0 and setting the ion current to zero, the electron saturation current density would be
Although this is the expression usually given in theoretical discussions of Langmuir probes, the derivation is not rigorous and the experimental basis is weak. The theory of double layers[1] typically employs an expression analogous to the Bohm criterion, but with the roles of electrons and ions reversed, namely
where the numerical value was found by taking Ti=Te and γi=γe. In practice, it is often difficult and usually considered uninformative to measure the electron saturation current experimentally. When it is measured, it is found to be highly variable and generally much lower (a factor of three or more) than the value given above. Often a clear saturation is not seen at all. Understanding electron saturation is one of the most important outstanding problems of Langmuir probe theory. Effects of the bulk plasmaDebye sheath theory explains the basic behavior of Langmuir probes, but is not complete. Merely inserting an object like a probe into a plasma changes the density, temperature, and potential at the sheath edge and perhaps everywhere. Changing the voltage on the probe will also, in general, change various plasma parameters. Such effects are less well understood than sheath physics, but they can at least in some cases be roughly accounted. Pre-sheathWe have noted that the Bohm criterion requires the ions to enter the Debye sheath at the sound speed. The potential drop that accelerates them to this speed is called the pre-sheath. It has a spatial scale that depends on the physics of the ion source but which is large compared to the Debye length and often of the order of the plasma dimensions. The magnitude of the potential drop is equal to (at least)
The acceleration of the ions also entails a decrease in the density, usually by a factor of about 2 depending on the details. ResistivityCollisions between ions and electrons will also affect the I-V characteristic of a Langmuir probe. When an electrode is biased to any voltage other than the floating potential, the current it draws must pass through the plasma, which has a finite resistivity. The resistivity and current path can be calculated with relative ease in an unmagnetized plasma. In a magnetized plasma, the problem is much more difficult. In either case, the effect is to add a voltage drop proportional to the current drawn, which shears the characteristic. The deviation from an exponential function is usually not possible to observe directly, so that the flattening of the characteristic is usually misinterpreted as a larger plasma temperature. Looking at it from the other side, any measured I-V characteristic can be interpreted as a hot plasma, where most of the voltage is dropped in the Debye sheath, or as a cold plasma, where most of the voltage is dropped in the bulk plasma. Without quantitative modeling of the bulk resistivity, Langmuir probes can only give an upper limit on the electron temperature. Sheath expansionIt is not enough to know the current density as a function of bias voltage, since it is the absolute current which is measured. In an unmagnetized plasma, the current-collecting area is usually taken to be the exposed surface area of the electrode. In a magnetized plasma, the projected area is taken, that is, the area of the electrode as viewed along the magnetic field. If the electrode is not shadowed by a wall or other nearby object, then the area must be doubled to account for current coming along the field from both sides. If the electrode dimensions are not small in comparison to the Debye length, then the size of the electrode is effectively increased in all directions by the sheath thickness. In a magnetized plasma, the electrode is sometimes assumed to be increased in a similar way by the ion Larmor radius. The finite Larmor radius allows some ions to reach the electrode that would have otherwise gone past it. The details of the effect have not been calculated in a fully self-consistent way. If we refer to the probe area including these effects as Aeff (which may be a function of the bias voltage) and make the assumptions
and ignore the effects of
then the I-V characteristic becomes
where
Magnetized plasmasThe theory of Langmuir probes is much more complex when the plasma is magnetized. The simplest extension of the unmagnetized case is simply to use the projected area rather than the surface area of the electrode. For a long cylinder far from other surfaces, this reduces the effective area by a factor of π/2 = 1.57. As mentioned before, it might be necessary to increase the radius by about the thermal ion Larmor radius, but not above the effective area for the unmagnetized case. The use of the projected area seems to be closely tied with the existence of a magnetic sheath. Its scale is the ion Larmor radius at the sound speed, which is normally between the scales of the Debye sheath and the pre-sheath. The Bohm criterion for ions entering the magnetic sheath applies to the motion along the field, while at the entrance to the Debye sheath it applies to the motion normal to the surface. This results in a reduction of the density by the sine of the angle between the field and the surface. The associated increase in the Debye length must be taken into account when considering ion non-saturation due to sheath effects. Especially interesting and difficult to understand is the role of cross-field currents. Naively, one would expect the current to flow parallel to the magnetic field along a flux tube. In many geometries, this flux tube will end at a surface in a distant part of the device, and this spot should itself exhibit an I-V characteristic. The net result would be the measurement of a double-probe characteristic, in other words, electron saturation current equal to the ion saturation current. When this picture is considered in detail, it is seen that the flux tube must charge up and the surrounding plasma must spin around it. The flow of current into or out of the flux tube must be associated with a force that slows down this spinning. Candidate forces are viscosity, friction with neutrals, and inertial forces associated with plasma flows, either steady or fluctuating. It is not known which force is strongest in practice, and in fact it is generally difficult to find any force that is powerful enough to explain the characteristics actually measured. It is also likely that the magnetic field plays a decisive role in determining the level of electron saturation, but no quantitative theory is as yet available. Electrode configurationsOnce one has a theory of the I-V characteristic of an electrode, one can proceed to measure it and then fit the data with the theoretical curve to extract the plasma parameters. The straightforward way to do this is to sweep the voltage on a single electrode, but, for a number of reasons, configurations using multiple electrodes and/or exploring only a part of the characteristic are used in practice. Single probeThe most straightforward way to measure the I-V characteristic of a plasma is with a single probe, consisting of one electrode biased with a voltage ramp relative to the vessel. The advantages are simplicity of the electrode and redundancy of information, i.e. one can check whether the I-V characteristic has the expected form. Potentially additional information can be extracted from details of the characteristic. The disadvantages are more complex biasing and measurement electronics and a poor time resolution. If fluctuations are present (as they always are) and the sweep is slower than the fluctuation frequency (as it usually is), then the I-V is the average current as a function of voltage, which may result in systematic errors if it is analyzed as though it were an instantaneous I-V. The ideal situation is to sweep the voltage at a frequenc above the fluctuation frequency but still below the ion cyclotron frequency. This, however, requires sophisticated electronics and a great deal of care.. Double probeAn electrode can be biased relative to a second electrode, rather than to the vessel. The theory is similar to that of a single probe, except that the current is limited to the ion saturation current for both positive and negative voltages. In particular, if Vbias is the voltage applied between two identical electrodes, we can write
which can be rewritten using Vbias = V2 − V1 as a hyperbolic tangent:
One advantage of the double probe is that that neither electrode is ever very far above floating, so the theoretical uncertainties at large electron currents are avoided. If it is desired to sample more of the exponential electron portion of the characteristic, an asymmetric double probe may be used, with one electrode larger than the other. The characteristic in this case is still a hyperbolic tangent, but shifted vertically. Another advantage is that there is no reference to the vessel, so it is to some extent immune to the disturbances in a radio frequency plasma. On the other hand, it shares the limitations of a single probe concerning complicated electronics and poor time resolution. In addition, the second electrode not only complicates the system, but it makes it susceptible to disturbance by gradients in the plasma. Triple probeAn elegant electrode configuration is the triple probe, consisting of two electrodes biased with a fixed voltage and a third which is floating. The bias voltage is chosen to be a few times the electron temperature so that the negative electrode draws the ion saturation current, which, like the floating potential, is directly measured. The positive tip draws a positive current equal in magnitude to the (normally negative) ion saturation current, so we can write
or
That is, the voltage difference between the positive and floating electrodes is proportional to the electron temperature. (This was especially important in the sixties and seventies before sophisticated data processing became widely available.) More sophisticated analysis of triple probe data can take into account such factors as incomplete saturation, non-saturation, unequal areas. Triple probes have the advantage of simple biasing electronics (no sweeping required), simple data analysis, excellent time resolution, and insensitivity to potential fluctuations (whether imposed by an rf source or inherent fluctuations). Like double probes, they are sensitive to gradients in plasma parameters. Special arrangementsArrangements with four (tetra probe) or five (penta probe) have sometimes been used, but the advantage over triple probes has never been entirely convincing. A pin-plate probe consists of a small electrode directly in front of a large electrode, the idea being that the voltage sweep of the large probe can perturb the plasma potential at the sheath edge and thereby aggravate the difficulty of interpreting the I-V characteristic. The floating potential of the small electrode can be used to correct for changes in potential at the sheath edge of the large probe. Experimental results from this arrangement look promising, but experimental complexity and residual difficulties in the interpretation have prevented this configuration from becoming standard. Various geometries have been proposed for use as ion temperature probes, for example, two cylindrical tips that rotate past each other im a magnetized plasma. Since shadowing effects depend on the ion Larmor radius, the results can be interpreted in terms of ion temperature. The ion temperature is an important quantity that is very difficult to measure. Unfortunately, it is also very difficult to analyze such probes in a fully self-consistent way. Emissive probes use an electrode heated either electrically or by the exposure to the plasma. When the electrode is biased more positive than the plasma potential, the emitted electrons are pulled back to the surface so the I-V characteristic is hardly changed. As soon as the electrode is biased negative with respect to the plasma potential, the emitted electrons are repelled and contribute a large negative current. The onset of this current or, more sensitively, the onset of a discrepancy between the characteristics of an unheated and a heated electrode, is a sensitive indicator of the plasma potential. To measure fluctuations in plasma parameters, arrays of electrodes are use, usually one- but occasionally two-dimensional. A typical array has a spacing of 1 mm and a total of 16 or 32 electrodes. A simpler arrangement to measure fluctuations is a negatively-biased electrode flanked by two floating electrodes. The ion-saturation current is taken as a surrogate for the density and the floating potential as a surrogate for the plasma potential. This allows a rough measurement of the turbulent particle flux
Practical considerationsFor laboratory and technical plasmas, the electrodes are most commonly tungsten wires several thousandths of an inch thick, because they have a high melting point but can be made small enough not to perturb the plasma. Although the melting point is somewhat lower, molybdenum is sometimes used because it is easier to machine and solder than tungsten. For fusion plasmas, graphite electrodes with dimensions from 1 to 10 mm are usually used because they can withstand the highest power loads (They not only withstand high temperature, when they do overheat, they sublimate rather than melt.), and the atoms that do get into the plasma result in less radiation due to the low atomic number of carbon. The electrode surface exposed to the plasma must be defined, e.g. by insulating all but the tip of a wire electrode. If there can be significant deposition of conducting materials (metals or graphite), then the insulator should be separated from the electrode by a meander to prevent short-circuiting. In a magnetized plasma, it appears to be best to choose a probe size a few times larger than the ion Larmor radius. A point of contention is whether it is better to use proud probes, where the angle between the magnetic field and the surface is at least 15°, or flush-mounted probes, which are embedded in the plasma-facing components and generally have an angle of 1 to 5 °. Many plasma physicists feel more comfortable with proud probes, which have a longer tradition and possibly are less perturbed by electron saturation effects, although this is disputed. Flush-mounted probes, on the other hand, being part of the wall, are less perturbative. Knowledge of the field angle is necessary with proud probes to determine the fluxes to the wall, whereas it is necessary with flush-mounted probes to determine the density. In very hot and dense plasmas, as found in fusion research, it is often necessary to limit the thermal load to the probe by limiting the exposure time. A reciprocating probe is mounted on an arm that is moved into and back out of the plasma, usually in about one second by means of either a pneumatic drive or an electromagnetic drive using the ambient magnetic field. Pop-up probes are similar, but the electodes rest behind a shield and are only moved the few millimeters necessary to bring them into the plasma near the wall. A Langmuir probe can be purchased off the shelf for on the order of 15,000 U.S. Dollars, or they can be built by an experienced researcher and/or technician. When working at frequencies under 100 MHz, it is advisable to use blocking filters, and take necessary grounding precautions. |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Langmuir_probe". A list of authors is available in Wikipedia. |





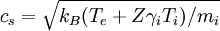 .
.
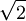 times smaller. Uncertainties of this magnitude arise several places in the analysis of Langmuir probe data and are very difficult to resolve.
times smaller. Uncertainties of this magnitude arise several places in the analysis of Langmuir probe data and are very difficult to resolve.
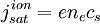
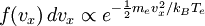 ,
,
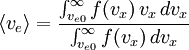 ,
,
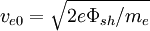 .
.
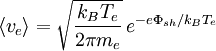 .
.
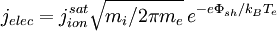 ,
,
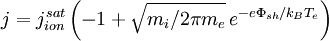 .
.
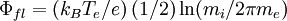 .
.
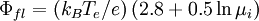
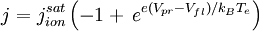 .
.
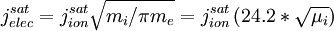
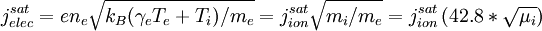
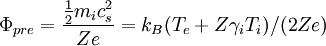
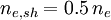 ,
,
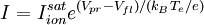 ,
,
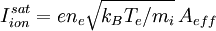 .
.
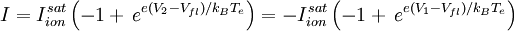 ,
,
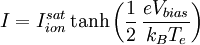 .
.
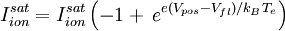 ,
,
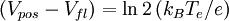 .
.