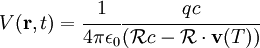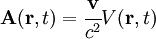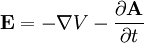Liénard-Wiechert Potentials

The Liénard-Wiechert potential describes the electromagnetic effect of a moving charge. Built directly from Maxwell's equations, this potential describes the complete, relativistically correct, time-varying electromagnetic field for a point-charge in arbitrary motion. These classical equations harmonize with the 20th century development of special relativity, but are not corrected for quantum-mechanical effects. Electromagnetic radiation in the form of waves are a natural result of the solutions to these equations.

These equations were developed in part by Emil Wiechert around 1898[1] and continued into the early 1900s.

The equations to solve for the electromagnetic effects make use of a vector potential and a scalar potential and can be generalized according to Gauge theory.

Additional recommended knowledge

Correct Test Weight Handling Guide: 12 Practical Tips

Daily Sensitivity Test

Implications

The study of classical electrodynamics was instrumental in Einstein's development of the theory of relativity. Analysis of the motion and propagation of electromagnetic waves led to the General relativity description of space and time. The Liénard–Wiechert formulation is an important launchpad into more complex analysis of relativistic moving particles.

The Liénard–Wiechert description is accurate for a large, independent moving particle, but breaks down at the quantum level.

Quantum mechanics sets important constraints on the ability of a particle to emit radiation. The classical formulation, as laboriously described by these equations, expressly violates experimentally observed phenomenon. For example, an electron around an atom does not emit radiation in the pattern predicted by these classical equations. Instead, it is governed by quantized principles regarding its energy state. In the later decades of the twentieth century, quantum electrodynamics helped bring together the radiative behavior with the quantum constraints.

Equations

Terms

r: The field point
t: The time
s(t): The position of the point charge (which, of course, may vary in time)
v(t): The velocity of point charge
T: The retarded time -- implicitly determined by the equation |r - s(T)| = c(t - T). Loosely speaking, the retarded time takes into account the time it takes for electromagnetic information to propagate from the source (point charge) to the observer (at the field point).

V: Scalar potential field
A: Vector potential field
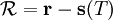$\mathcal{R} = \mathbf{r} - \mathbf{s}(T)$ (or its magnitude, as will be clear from context)